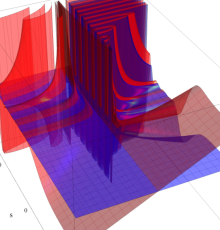
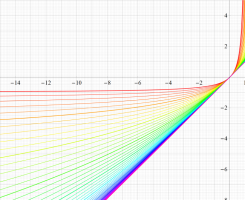
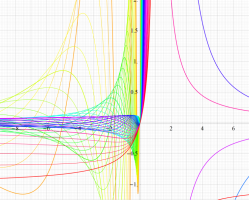
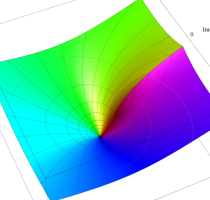
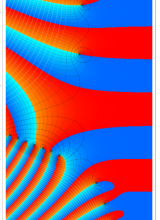
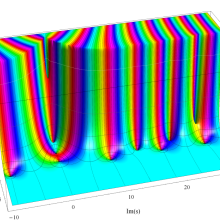
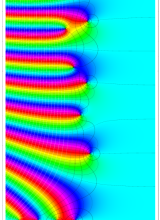
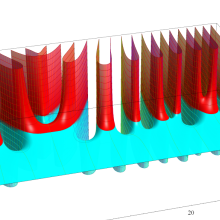
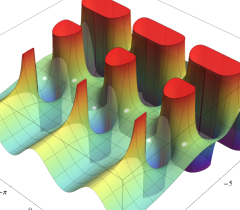
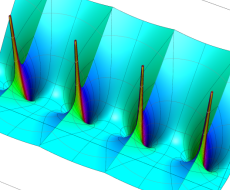
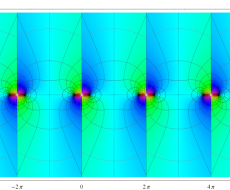
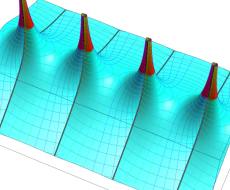
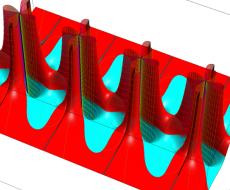
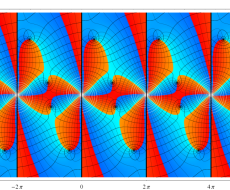
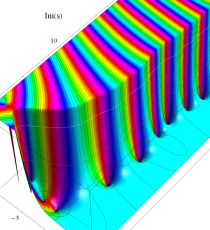
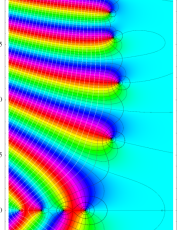
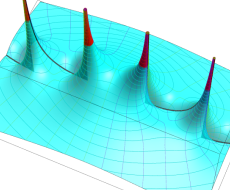
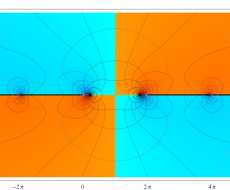
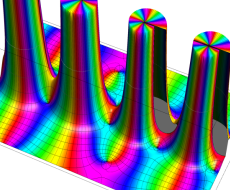
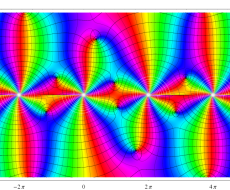
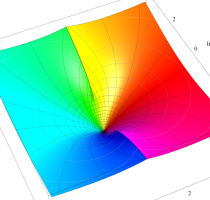
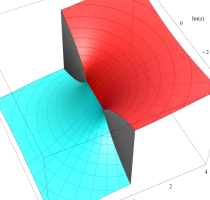
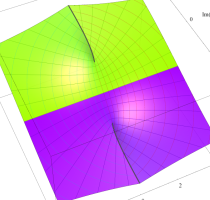
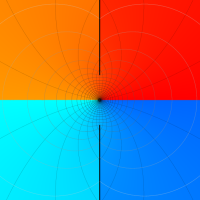
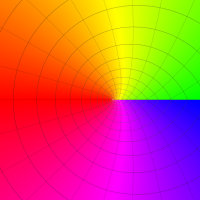
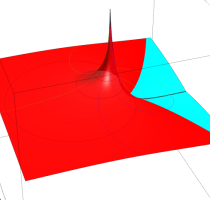
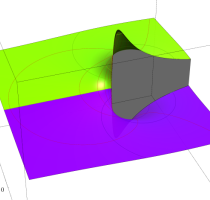
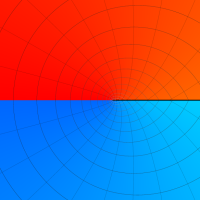
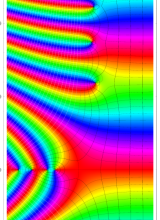
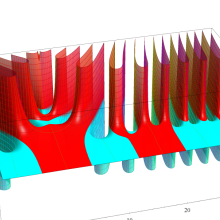
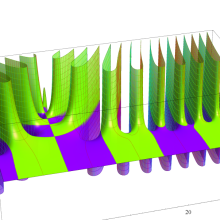
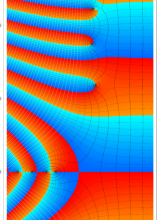
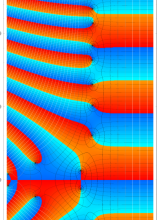
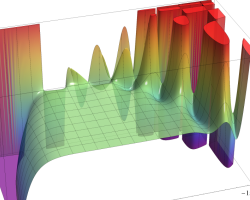
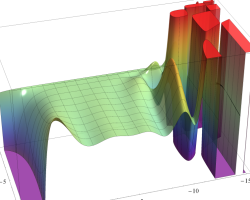
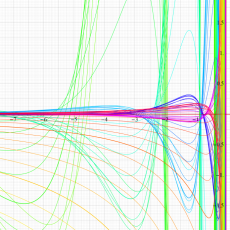
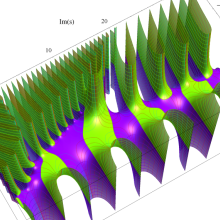
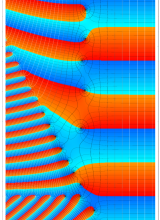
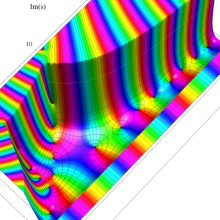
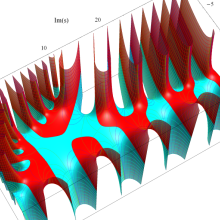
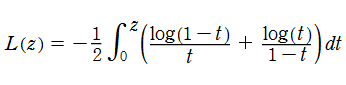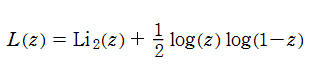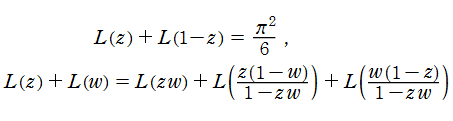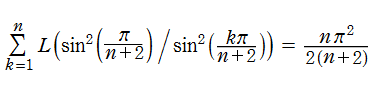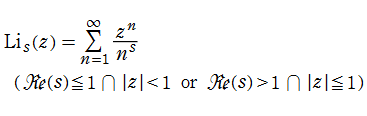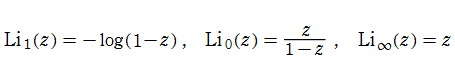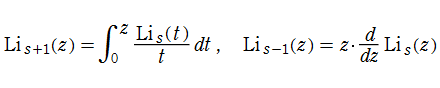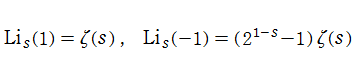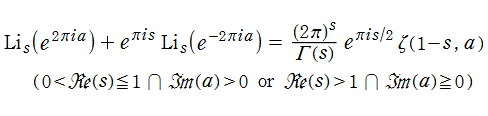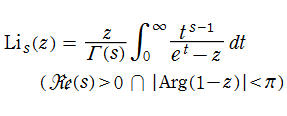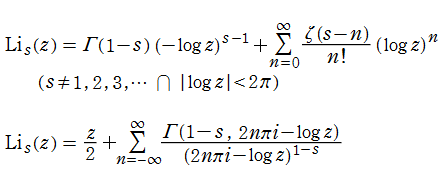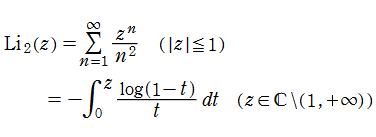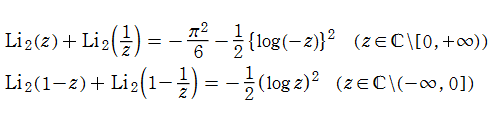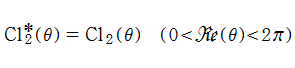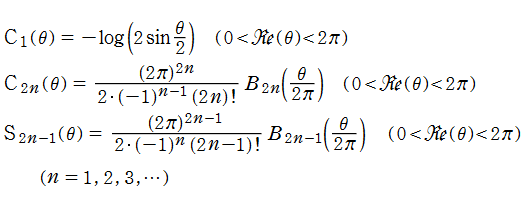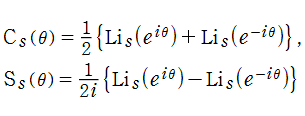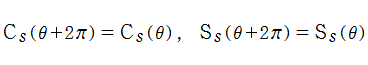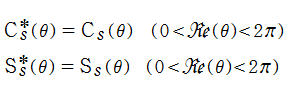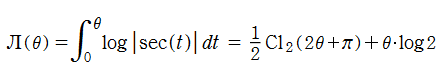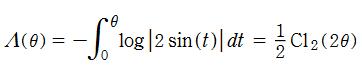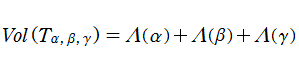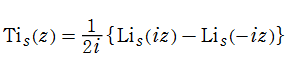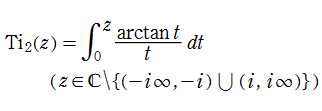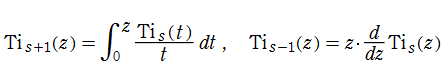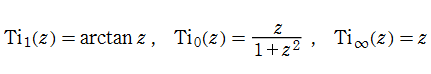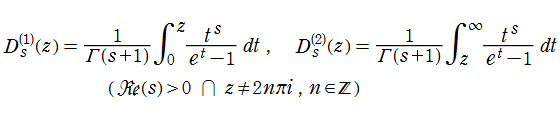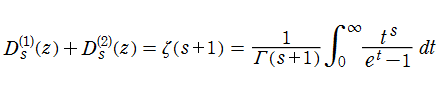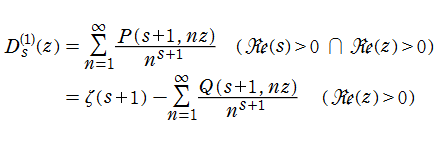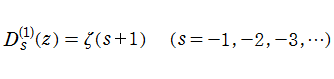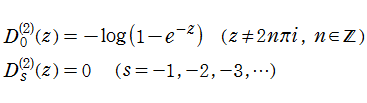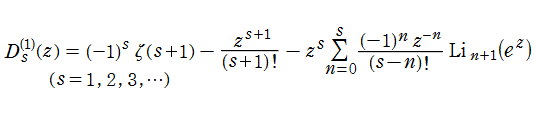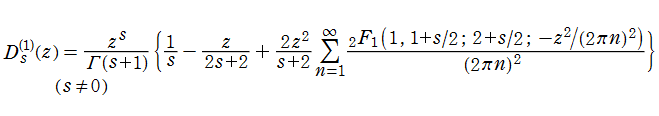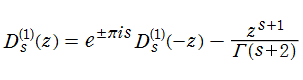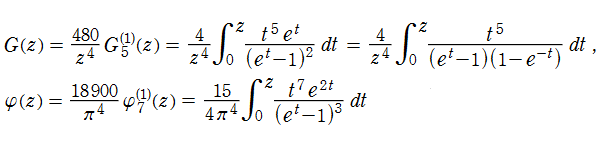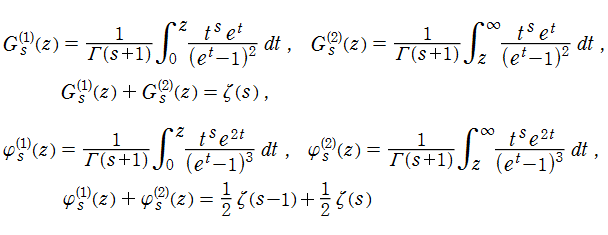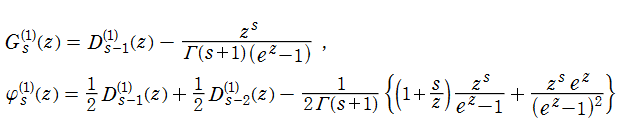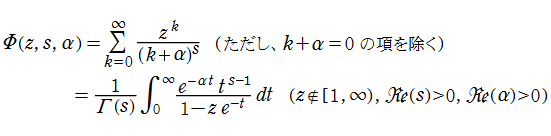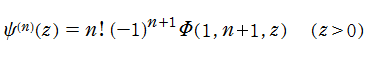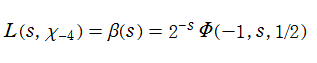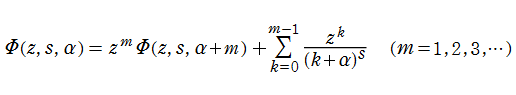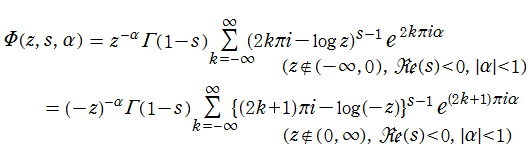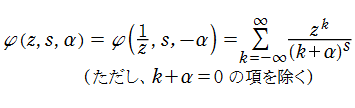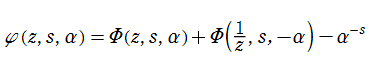特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
ポリ対数関数(多重対数関数)
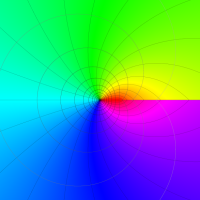
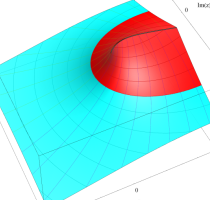
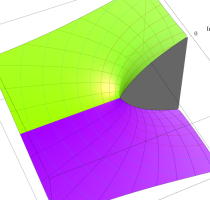
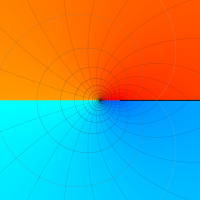
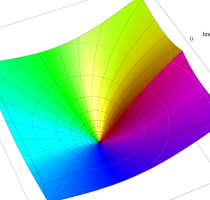
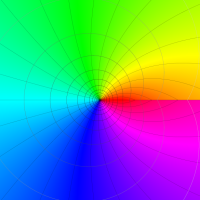
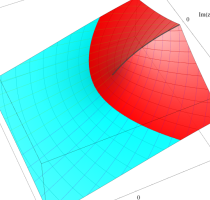
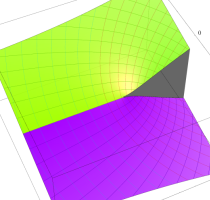
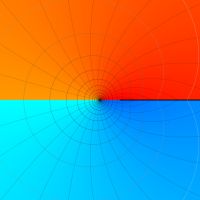
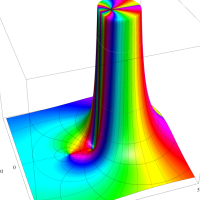
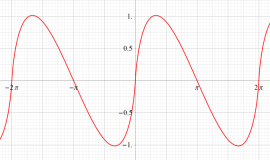
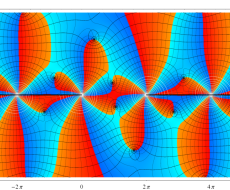
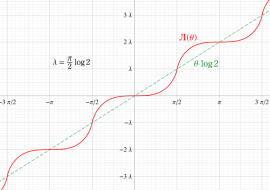
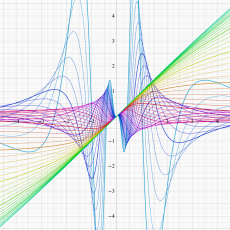
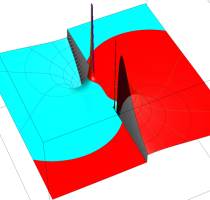
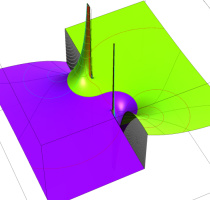
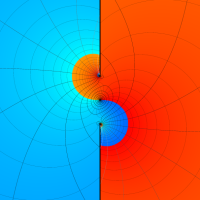
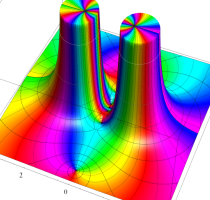
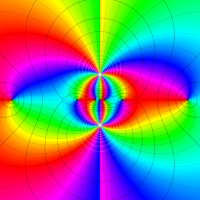
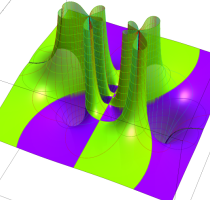
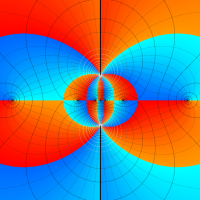
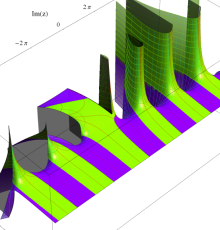
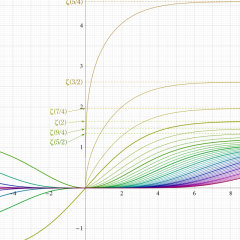
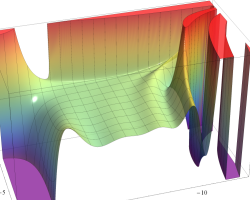
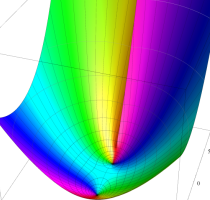
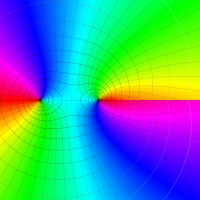
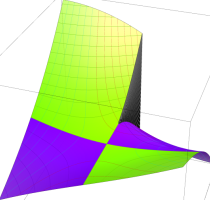
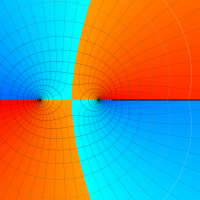
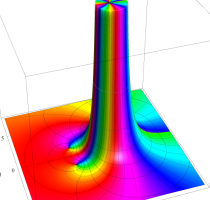
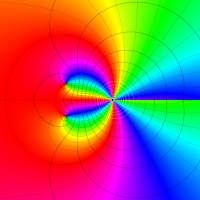
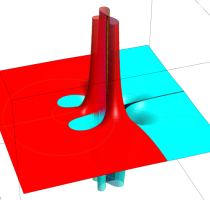
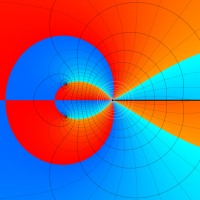
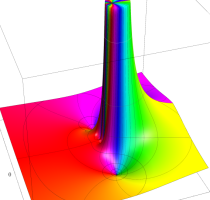
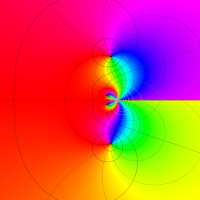
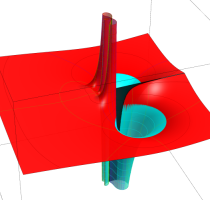
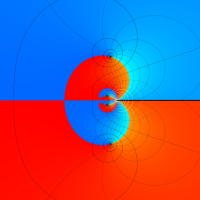
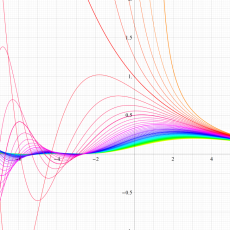
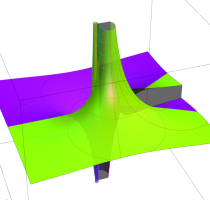
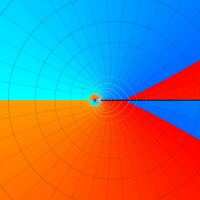
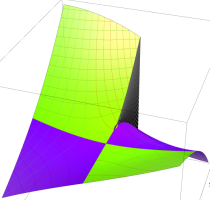
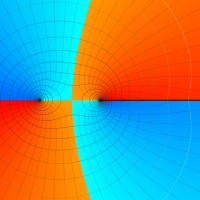
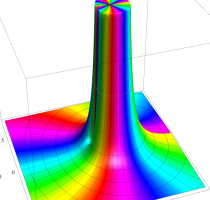
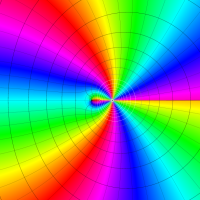
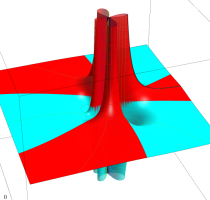
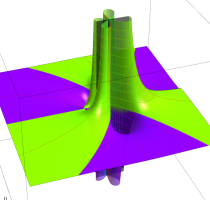
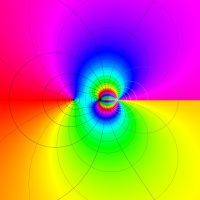
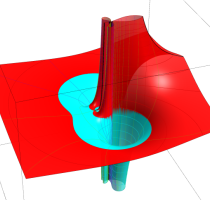
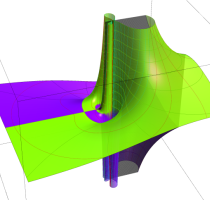
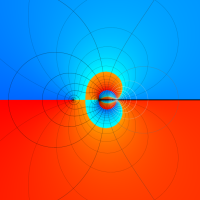
Rogers の二重対数関数
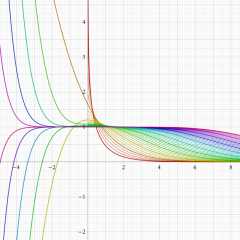
Rogers の二重対数関数は、対数関数を拡張したものでで定義される。後述のポリ対数関数とは
の関係にある。また、関数等式
を満たし、特殊値
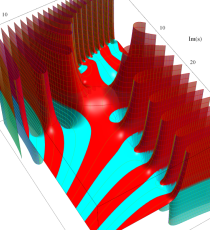
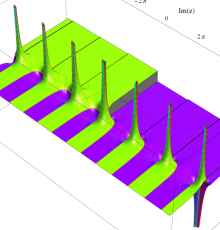
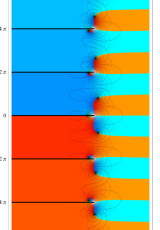
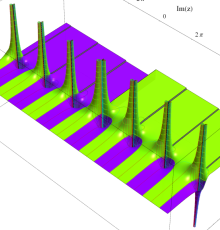
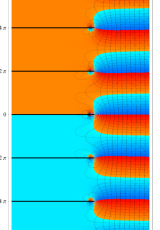
を持つことで知られる。複素関数としての Rogers の二重対数関数は、複素平面上
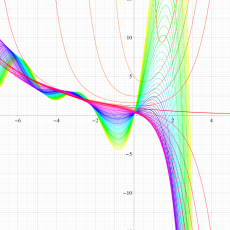
ポリ対数関数
日:ポリ対数関数,多重対数関数英:Polylogarithm,仏:Fonction polylogarithme,独:Polylogarithmus
冪級数で定義された
を、収束範囲の外部にも解析接続して得られる関数を、ポリ対数関数、または多重対数関数という。その名称は、特別な
となり、他方で一般の
となることから、
に還元される。また、
を介して、Hurwitz のゼータ関数とも関係がある。
ポリ対数関数は
等、多くの積分表示式が知られており、応用分野ではそれらの表示形が重要になる (例えば、NISTの25.12(iii)など)。
また、無限級数表示
等も多数得られている。特に後者は、特異点を除く
ポリ対数関数は、後述する Lerch の超越関数の特別な場合であり、
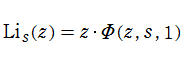
ポリ対数関数は、1889年に A. Jonquière が、経路積分を用いて複素関数としての
は、G. W. Leibniz が初めて考察して以降、L. Euler (1768年)、W. Spence (1809年) 等、多くの数学者がこれを手掛けた※1。前述の Rogers の二重対数関数もこのような研究の一端として現れた。
を満たし、諸公式で出現する頻度がより高いので重要である。
ポリ対数関数の数学における応用分野として、数論、コホモロジー (cohomology) を用いる群論、代数的K理論等が知られている。諸科学では、電気回路設計、量子電磁気学における Feynman ダイアグラムでの積分等の応用事例がある。
【註記】
※1: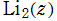 は、Spence の寄与に因んで 「Spence's function」 と呼ばれることもあるが、英語・日本語ともに 「dilogarithm (ディ・ロガリズム:二重対数)」 と呼ぶことの方が多い。後者の名称は、1828年に C. J. Hill が初めて使用した。また、これに準じて
は、Spence の寄与に因んで 「Spence's function」 と呼ばれることもあるが、英語・日本語ともに 「dilogarithm (ディ・ロガリズム:二重対数)」 と呼ぶことの方が多い。後者の名称は、1828年に C. J. Hill が初めて使用した。また、これに準じて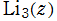 を 「trilogarithm (トリ・ロガリズム:三重対数)」 と呼ぶことがある。
を 「trilogarithm (トリ・ロガリズム:三重対数)」 と呼ぶことがある。
※1:
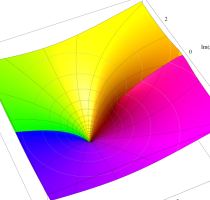
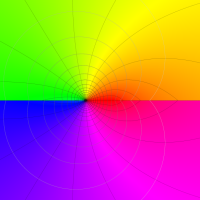
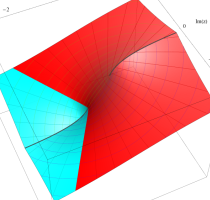
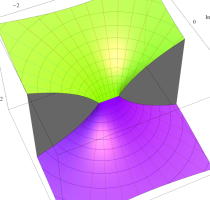
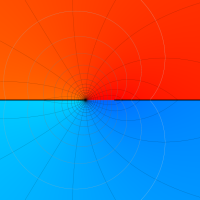
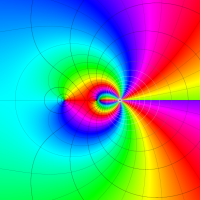
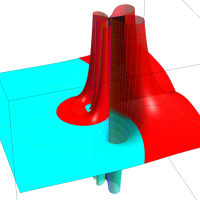
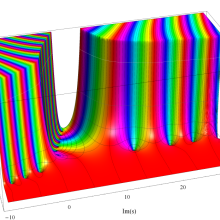
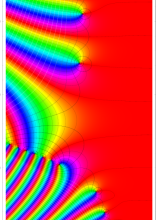
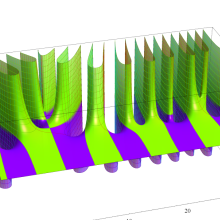
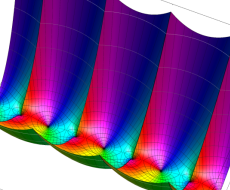
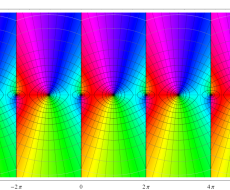
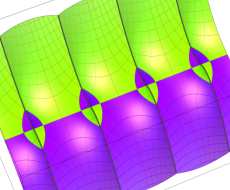
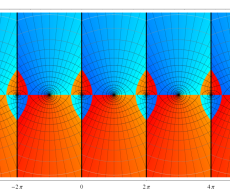
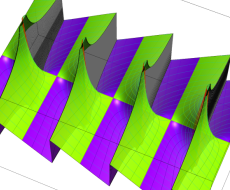
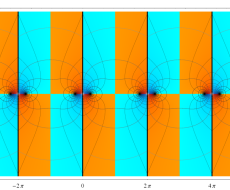
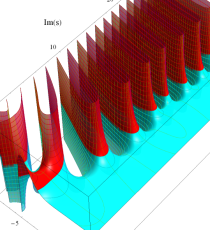
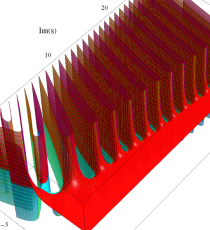
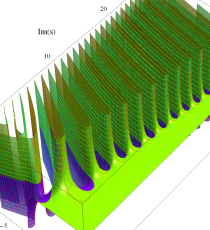
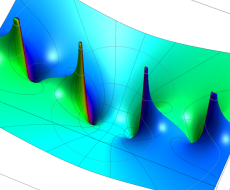
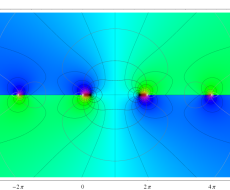
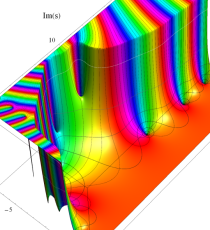
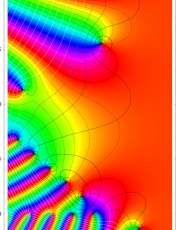
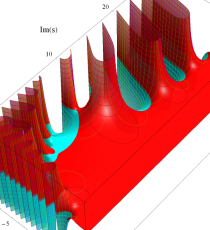
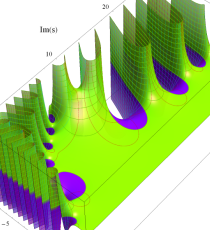
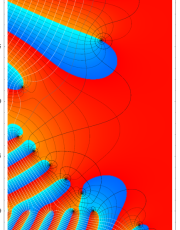
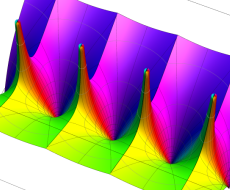
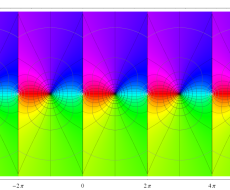
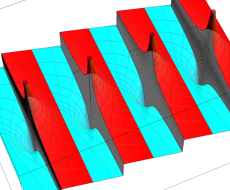
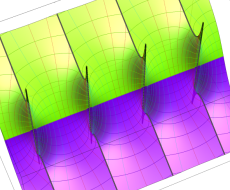
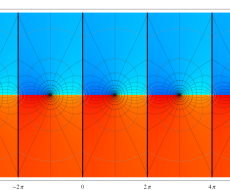
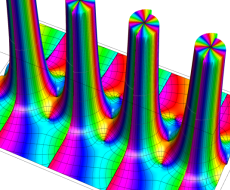
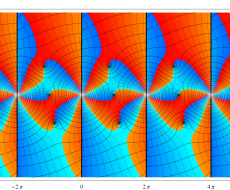
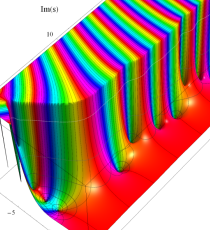
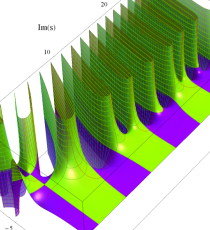
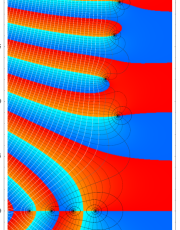
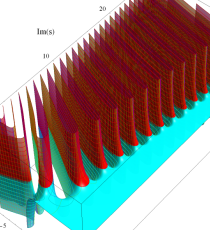
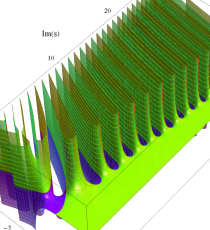
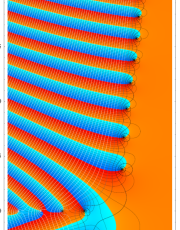
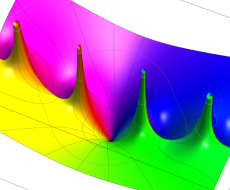
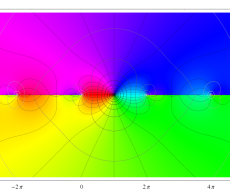
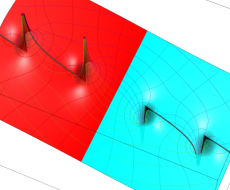
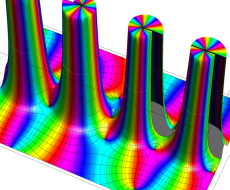
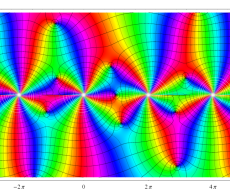
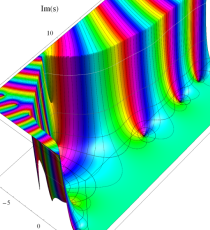
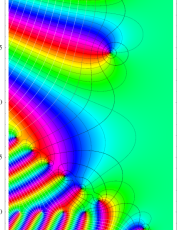
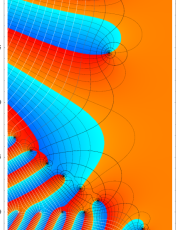
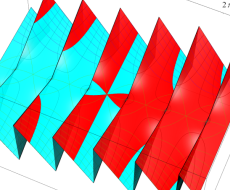
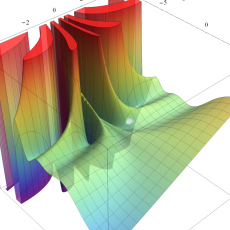
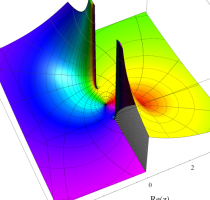
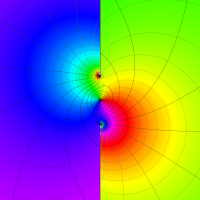
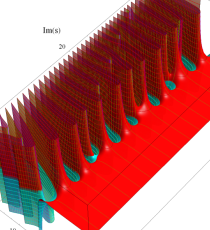
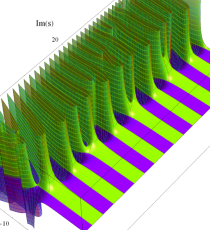
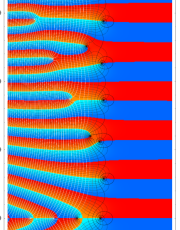
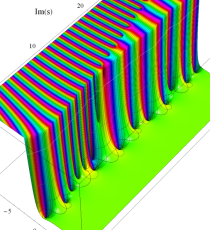
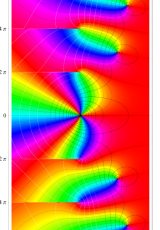
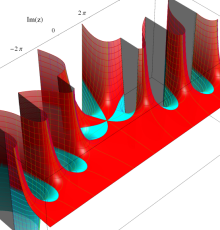
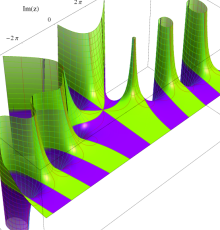
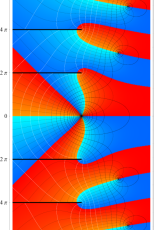
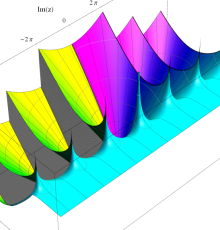
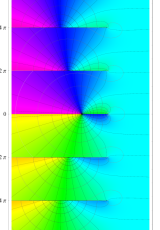
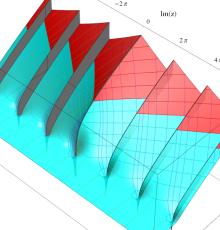
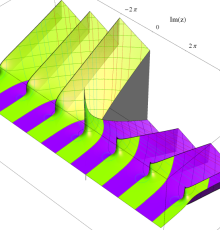
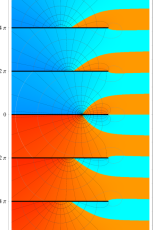
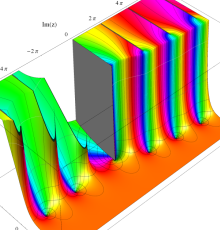
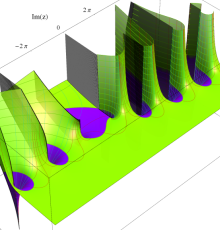
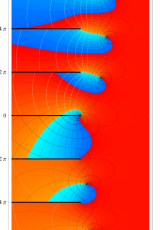
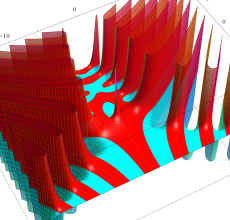
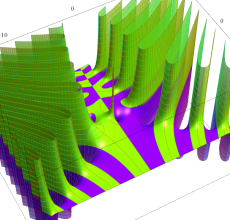
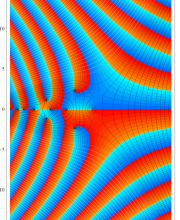
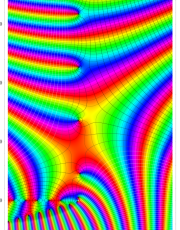
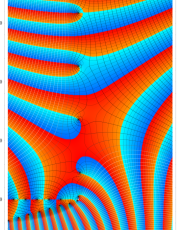
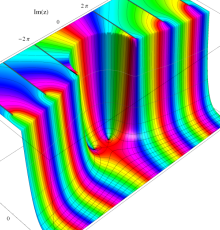
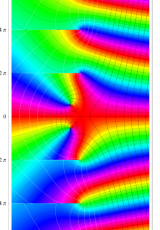
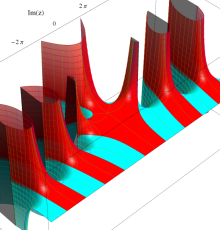
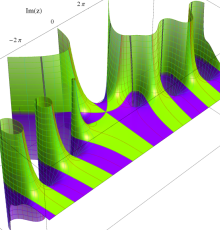
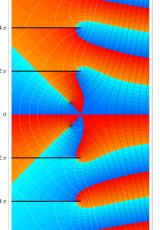
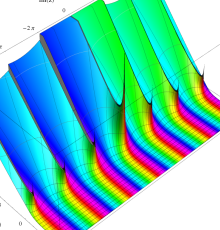
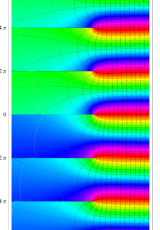
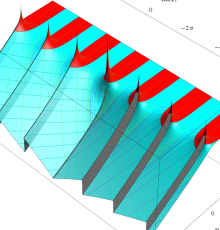
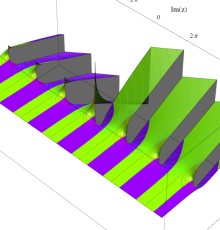
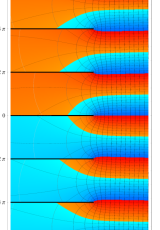
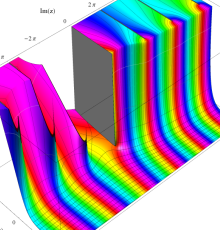
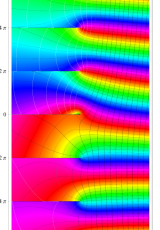
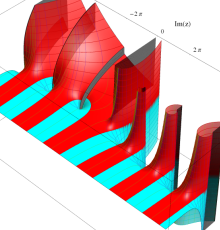
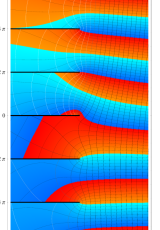
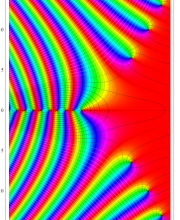
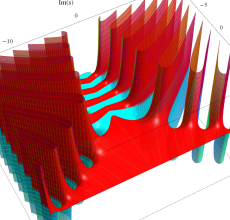
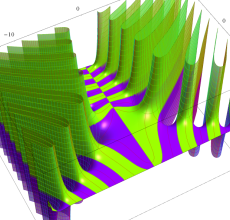
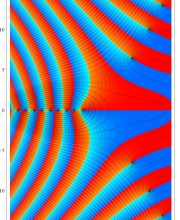
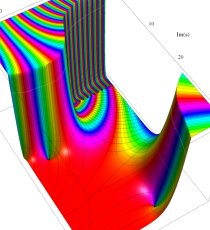
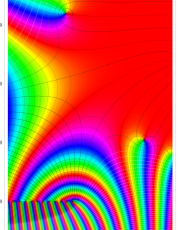
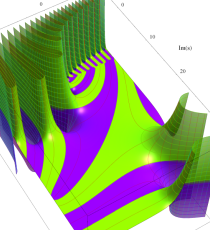
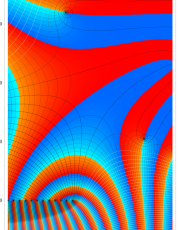
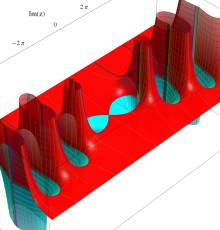
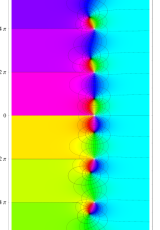
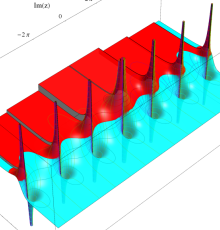
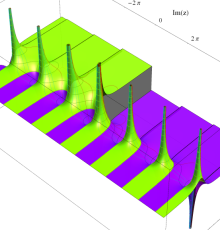
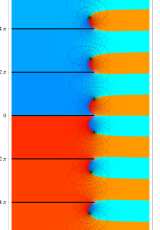
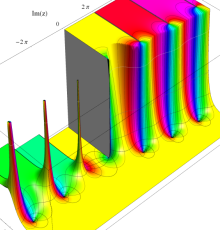
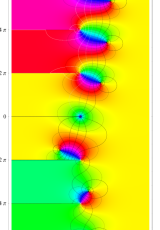
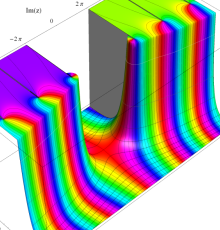
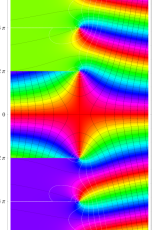
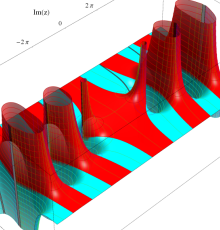
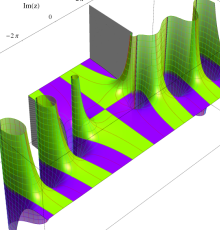
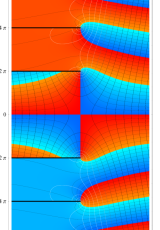
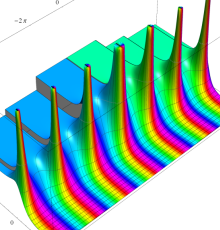
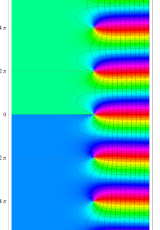
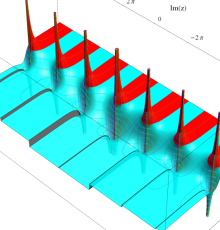
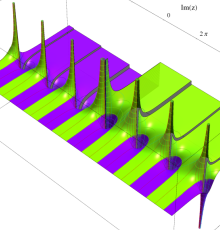
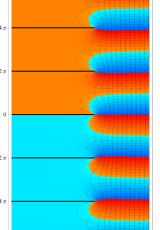
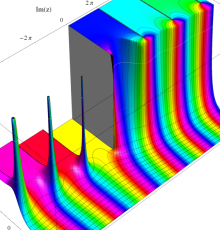
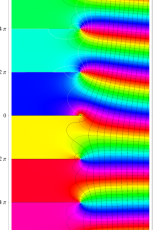
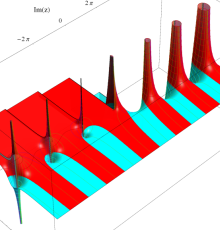
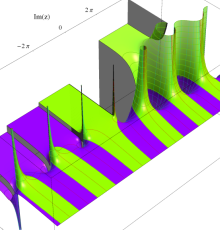
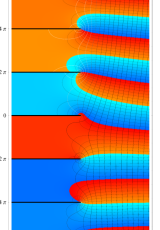
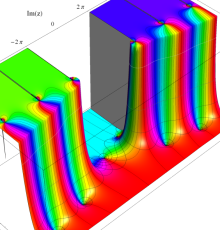
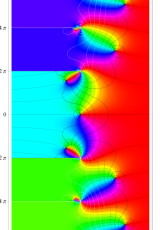
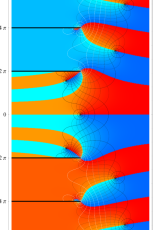
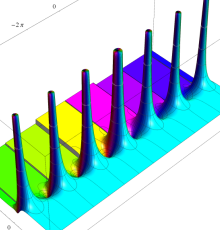
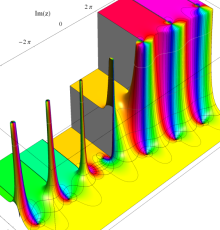
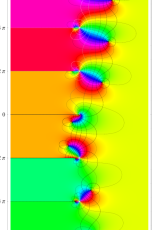
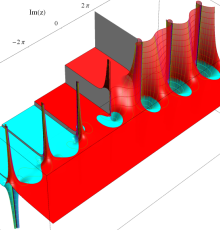
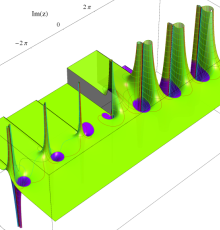
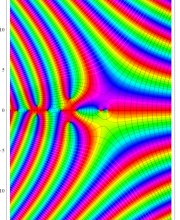
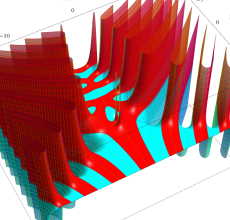
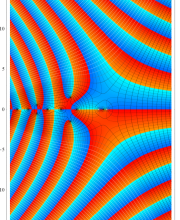
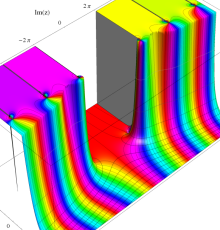
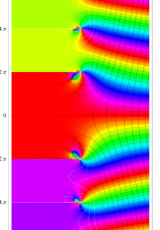
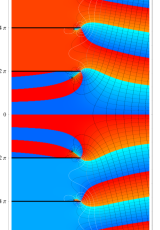
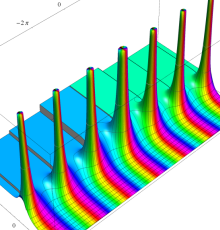
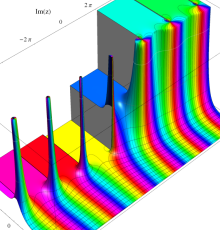
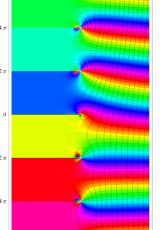
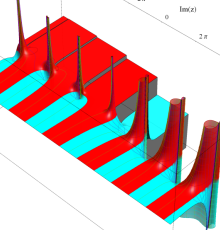
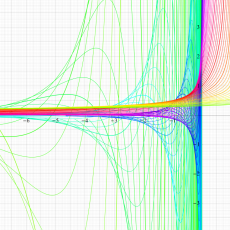
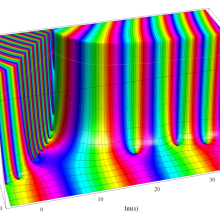
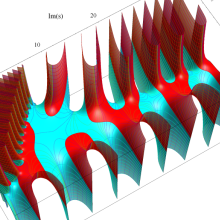
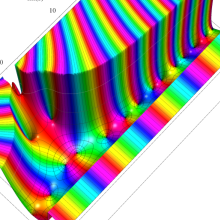
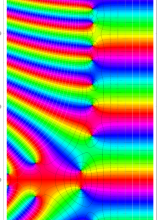
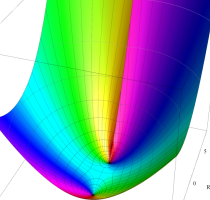
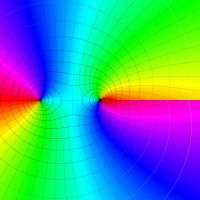
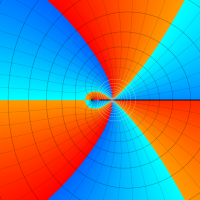
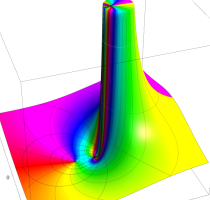
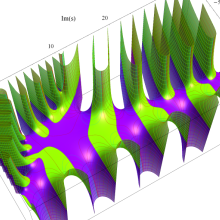
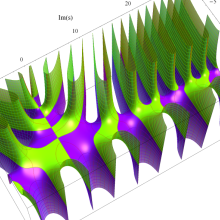
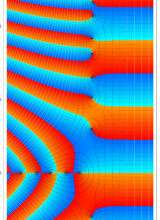
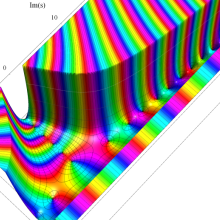
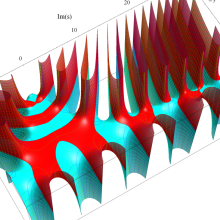
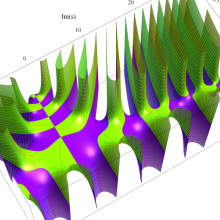
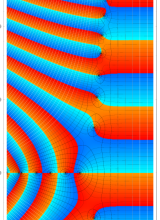
複素変数のポリ対数関数
複素変数のポリ対数関数
複素変数のポリ対数関数
複素変数のポリ対数関数
複素変数のポリ対数関数
複素変数のポリ対数関数
アニメーション(5.10MB)
複素変数のポリ対数関数
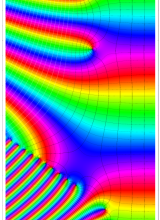
Clausen 関数
日:Clausen関数,クラウゼン関数英:Clausen function,仏:Fonction de Clausen,独:Clausen-funktion
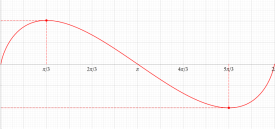
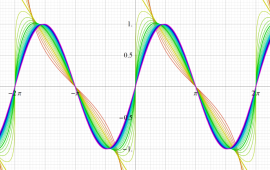
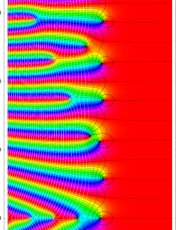
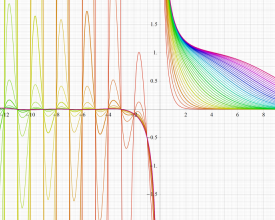
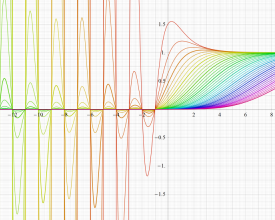
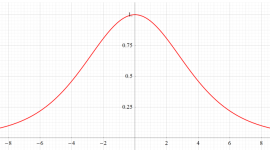
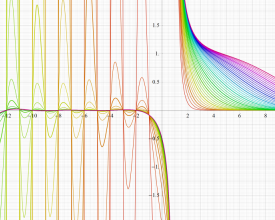
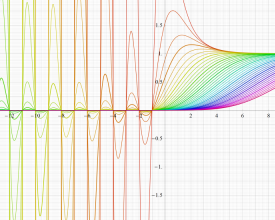
簡単な形の Fourier 級数が初等関数にならない具体例として、1832年に T. Clausen は
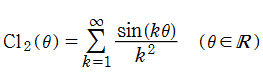
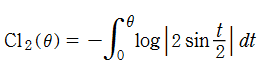
Clausen 関数は奇関数で、周期性
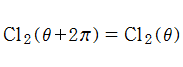
このため当サイトでは、実軸上の区間
となるが、もはや周期性を持たず、実変数のときは区間
現在では、前述の Fourier 級数表示式を一般化した
も定義されており、「一般 Clausen 関数」 と呼ばれている。このとき、記号の対応が
次数
と表わされ、初等関数に還元される。
一般 Clausen 関数は、ポリ対数関数を用いて
と表わされる。つまり、これは Euler の公式の類似であり、
を持つ。複素関数としては両者とも
このため当サイトでは、
となるが、もはや周期性を持たず、実変数のときは区間
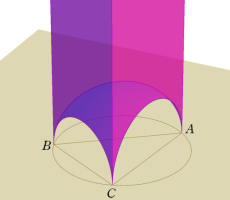
N. I. Lobachevsky は (J. Bolyai, J. C. F. Gauss 等と独立に) 双曲的非 Euclid 幾何学を構築する過程で、三次元双曲的非 Euclid 空間内の理想四面体
を1829年に導入した。現在では、これと若干形が異なる
を、Lobachevsky 関数と呼ぶことが多い。実際、前述の体積は
と表わした方が簡潔になる。(しかしながら、当サイトでは
実軸上
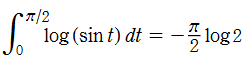
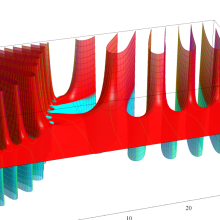
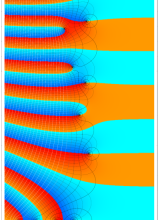
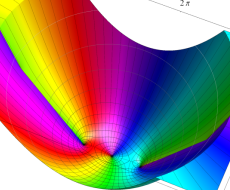
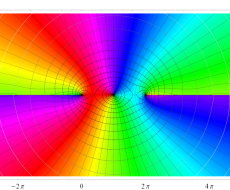
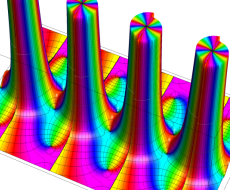
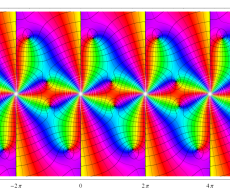
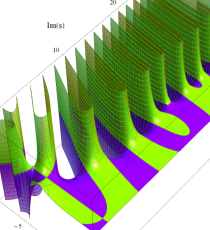
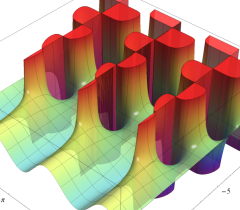
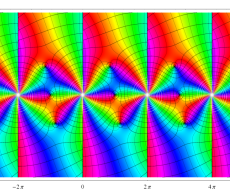
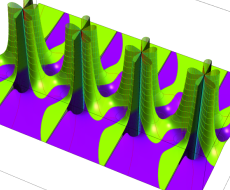
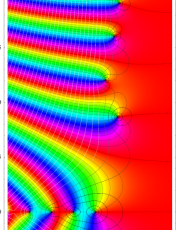
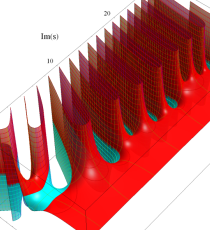
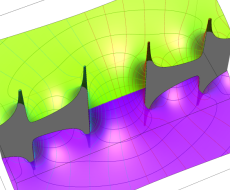
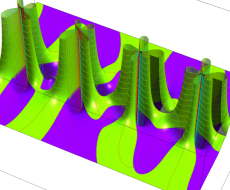
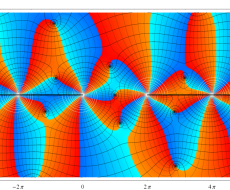
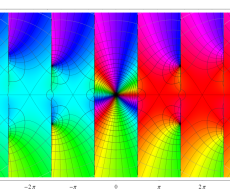
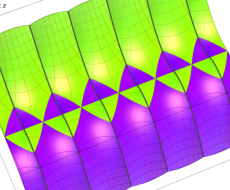
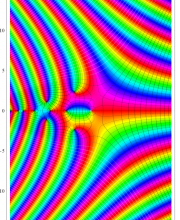
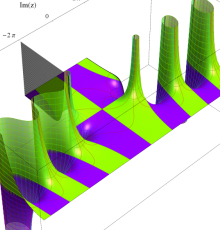
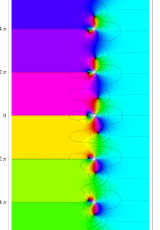
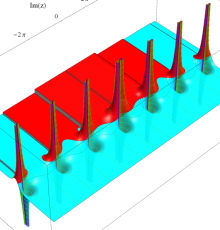
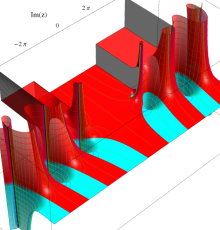
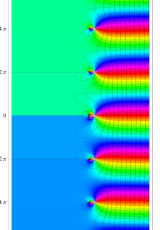
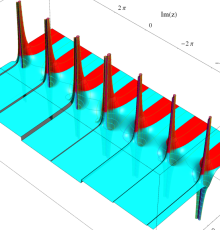
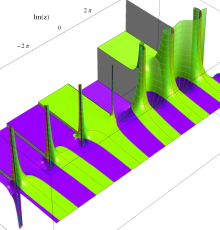
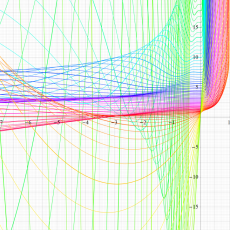
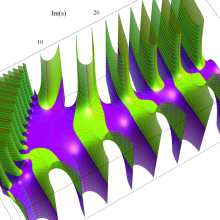
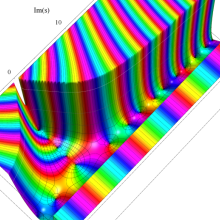
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
因みに、この例は
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
因みに、この例は
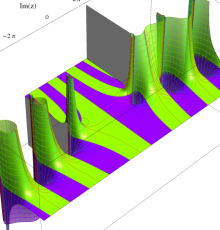
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の一般 Clausen 関数
複素変数の Lobachevsky 関数
積分逆正接関数
日:積分逆正接関数,逆正接積分英:Inverse tangent integral,仏:Arc tangente intégral,独:Integral Arkustangens
ポリ対数関数を用いて定義された
を、一般積分逆正接関数といい、その特別な場合の
を、(本来の) 積分逆正接関数という。
一般積分逆正接関数が、逐次積分・微分による
を満たすこと、および特別な
となること等、その性質の多くはポリ対数関数から導ける。同様に、
一般積分逆正接関数は、後述する Lerch の超越関数の特別な場合であり、
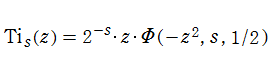
一般積分逆正接関数は L. Lewin (1958年) の研究によって、ほぼ現在の形に整備されたが、同種の関数はもっと古くから研究されていたと思われる。実際、
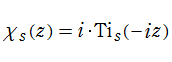
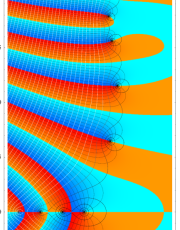
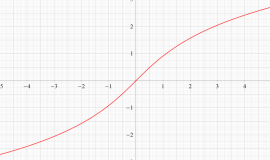
複素変数の積分逆正接関数
複素変数の一般積分逆正接関数
複素変数の一般積分逆正接関数
複素変数の一般積分逆正接関数
複素変数の一般積分逆正接関数
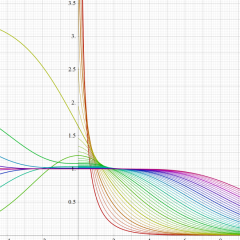
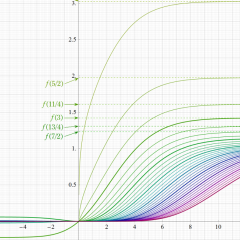
Debye 関数
日:Debye関数,デバイ関数,不完全ゼータ関数英:Debye function,仏:Fonction de Debye,独:Debye-funktion
Debye 関数とは、積分
で定義される関数の総称で、前者は 第1種- 、後者は 第2種- を冠して呼ばれる。(定数因子
両者は互いに
の関係にあるが、これは不完全ガンマ関数のそれと類似しており、しかも、右辺が Riemann ゼータ関数になるので、Debye 関数を 「不完全ゼータ関数」 と呼ぶこともある※1。また、冒頭の積分表示式から、正則化不完全ガンマ関数を係数とする Dirichlet 級数
に展開できることが分かる。すなわち、Debye 関数は
となる。第2種 Debye 関数の場合は
となり、特に
で表わすことができる。一般の
によって計算できる。これらの式におけるポリ対数関数および超幾何関数部分は、註記(※2)で説明している分枝切断線処理に応じて解析接続が必要になる。なお、分枝切断線が 「タイプ2」 となる解析接続は、代わりに
を用いても実現できる。
Debye 関数は、種々の積分計算に用いられるほか、物理学では黒体放射や固体の温度に関する量子力学などに現れる (多くは
他にも、Debye 関数に関連した積分関数として、E. Grüneisen による種々の温度下における物質の電気抵抗率を評価する研究から Grüneisen 関数
が導入されている。
ここでは、次の一般的な形で第1種 Grüneisen 関数
ただし、これらの関数は Debye 関数と初等関数を用いて、
と表わせる。この事は、積分表示式に部分積分法を適用すれば容易に確認できる。
【註記】
※1:次の論文では、不完全ゼータ関数 (すなわち Debye 関数) の詳しい数値計算結果、特に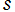 を複素変数とする場合の結果が載っている (ただし、関数記号等は当サイトと異なる)。
を複素変数とする場合の結果が載っている (ただし、関数記号等は当サイトと異なる)。
① K. S. Kölbig 「Complex zeros of an Incomplete Riemann zeta function and of the Incomplete gamma function」 Mathematics of Computation, Vol.24, No.111, (1970) p.679-696
② K. S. Kölbig 「Complex zeros of two Incomplete Riemann zeta functions」 Mathematics of Computation, Vol.26, No.118, (1972) p.551-565
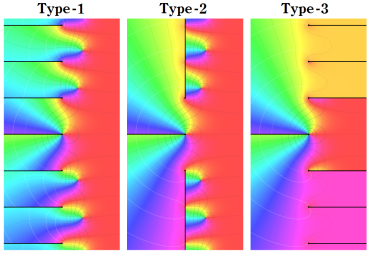
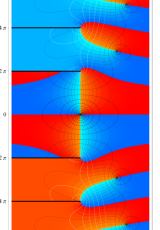
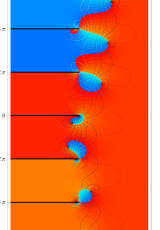
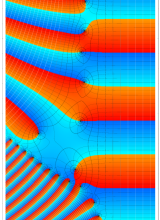
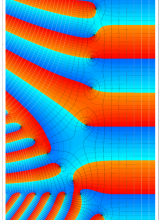
※2:コード 「Zeta. m」 では、次の3種類の分枝切断線が選択できる (グラフは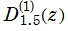 の場合)。当サイトでは、タイプ1の分枝切断線を採用する。
の場合)。当サイトでは、タイプ1の分枝切断線を採用する。
※1:次の論文では、不完全ゼータ関数 (すなわち Debye 関数) の詳しい数値計算結果、特に
① K. S. Kölbig 「Complex zeros of an Incomplete Riemann zeta function and of the Incomplete gamma function」 Mathematics of Computation, Vol.24, No.111, (1970) p.679-696
② K. S. Kölbig 「Complex zeros of two Incomplete Riemann zeta functions」 Mathematics of Computation, Vol.26, No.118, (1972) p.551-565
※2:コード 「Zeta. m」 では、次の3種類の分枝切断線が選択できる (グラフは
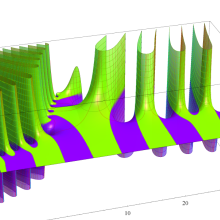
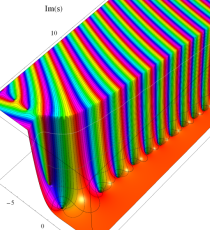
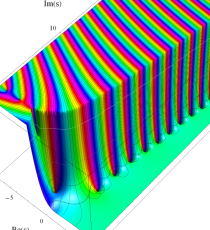
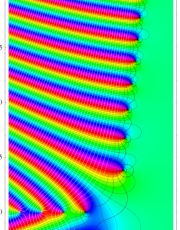
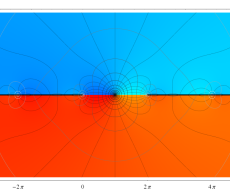
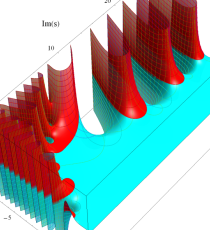
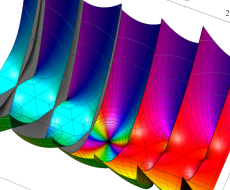
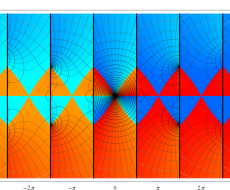
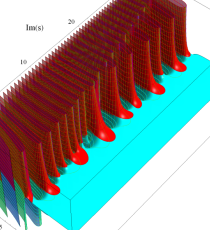
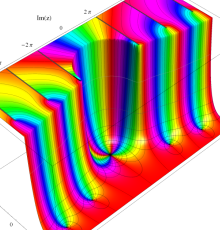
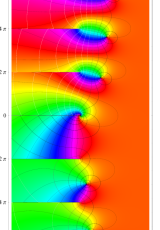
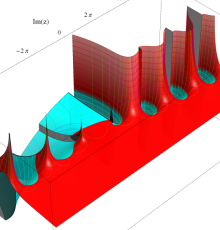
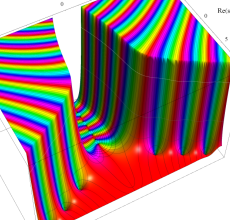
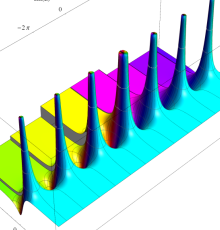
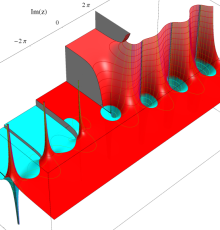
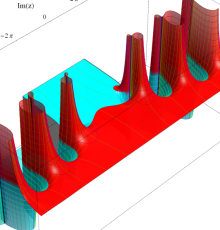
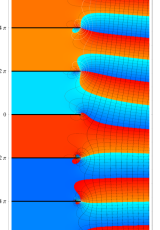
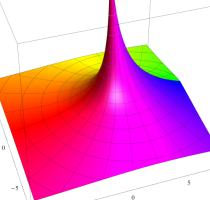
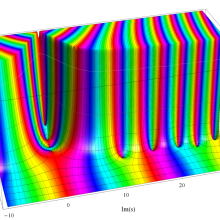
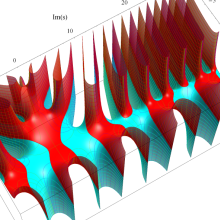
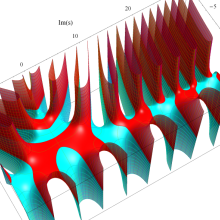
複素変数の第1種 Debye 関数
複素変数の第1種 Debye 関数
複素変数の第1種 Debye 関数
アニメーション(15.8MB)
複素変数の第1種 Debye 関数
(FunctionPlot.m のカラーリングを使用しています。)
公式からも明らかなように、
複素変数の第1種 Debye 関数
複素変数の第1種 Debye 関数
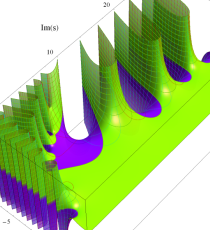
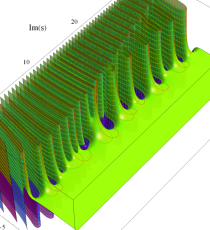
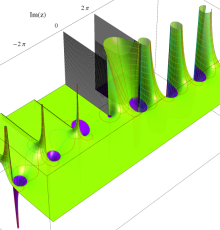
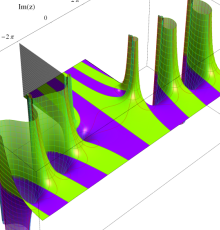
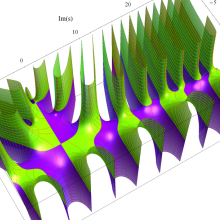
複素変数の第2種 Debye 関数
複素変数の第2種 Debye 関数
複素変数の第2種 Debye 関数
複素変数の第2種 Debye 関数
複素変数の第2種 Debye 関数
また、
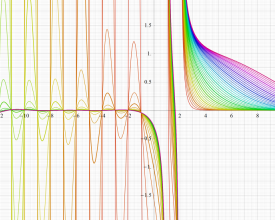
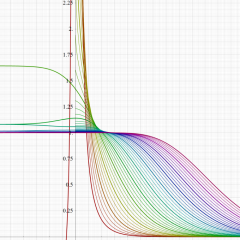
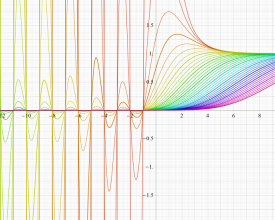
実変数の Grüneisen 関数
複素変数の第1種 Grüneisen 関数
(もし、タイプ2の分枝切断線を採用したならば、描画領域全体で
複素変数の第1種 Grüneisen 関数
複素変数の第1種 Grüneisen 関数
また、
複素変数の第2種 Grüneisen 関数
(もし、タイプ2の分枝切断線を採用したならば、描画領域全体で
複素変数の第2種 Grüneisen 関数
複素変数の第2種 Grüneisen 関数
複素変数の第1種 Strömgren 関数
複素変数の第1種 Strömgren 関数
複素変数の第1種 Strömgren 関数
複素変数の第1種 Strömgren 関数
複素変数の第1種 Strömgren 関数
第2種 Strömgren 関数は、
複素変数の第2種 Strömgren 関数
複素変数の第2種 Strömgren 関数
複素変数の第2種 Strömgren 関数
Lerch の超越関数
日:Lerchの超越関数,レルヒ超越関数,Lerchのゼータ関数英:Lerch transcendents,仏:Fonctions transcendantes de Lerch,独:Lerchsche Zetafunktion
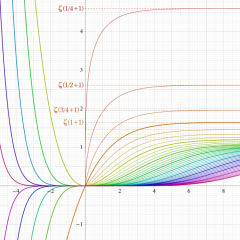
ポリ対数関数と Hurwitz のゼータ関数を統合・一般化した、
を Lerch の超越関数、あるいは単に Lerch 関数という。さらに、Lerch の超越関数はポリガンマ関数の一般化にもなっていて、
となる。
Dirichlet のL関数は、Lerch の超越関数を用いて表わすことができる。例えば、Catalan のベータ関数とも呼ばれる Dirichlet のL関数の例は
である。
Lerch の超越関数は、各引数について解析接続を可能にする多くの公式が知られている。例えば、引数
を満たす。また、
は、数値計算の際に便利である。
なお、異なる無限和の取り方によって
が定義される。
となる。
Lerch の超越関数なる名称は、1887年の M. Lerch による研究結果に因むが、それ以前にも、C. J. Malmstén (1849年)、R. Lipschitz (1857年, 1887年) 等の研究事例がある。
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数
複素変数の Lerch の超越関数