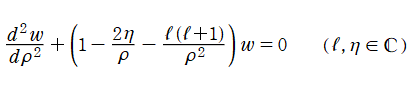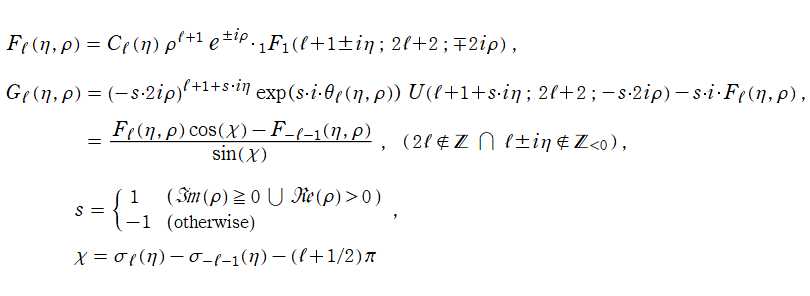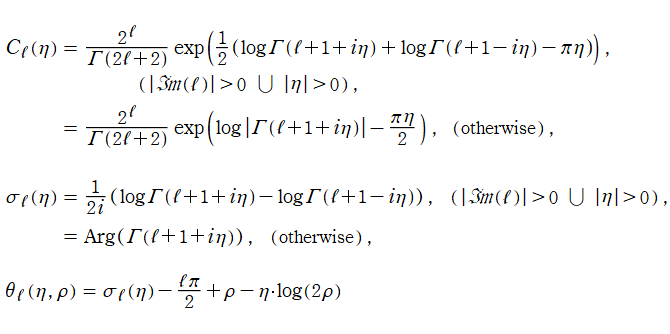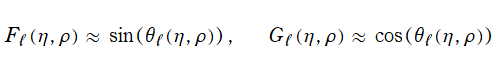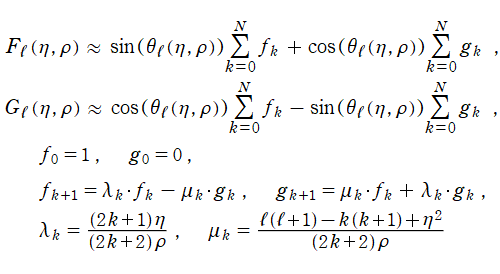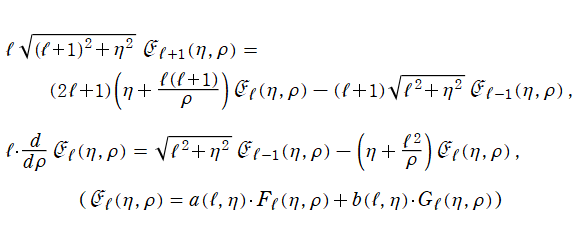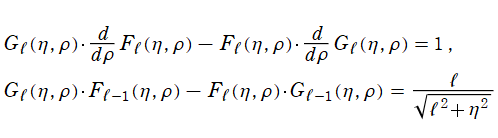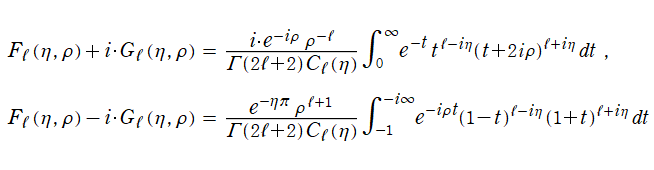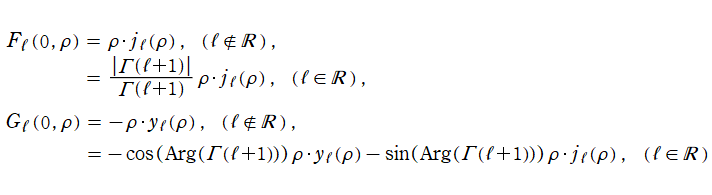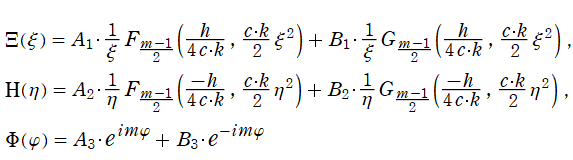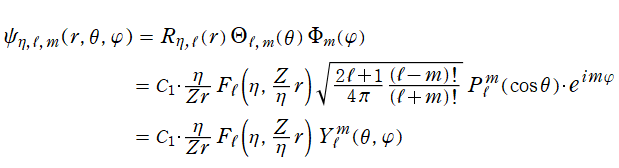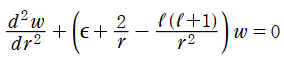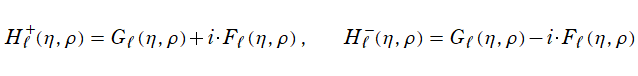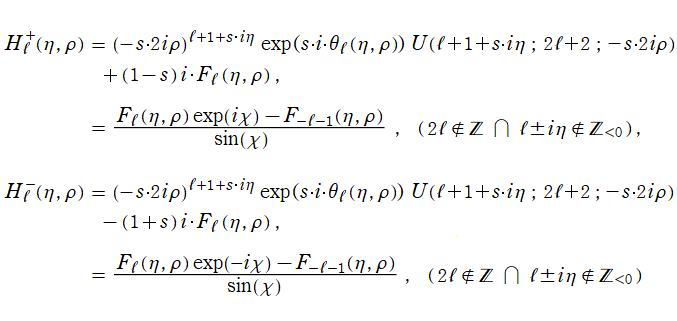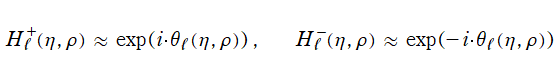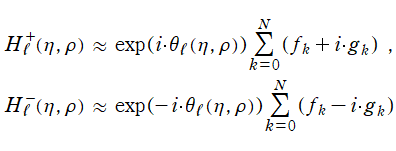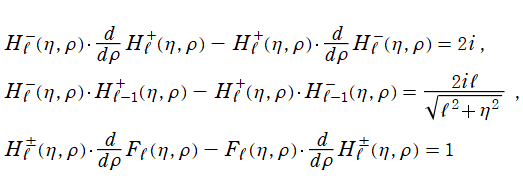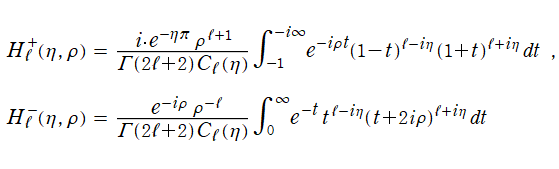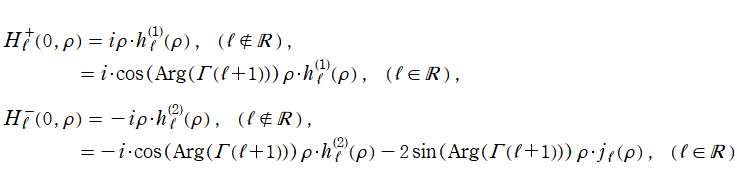Coulomb 波動関数
日:
Coulomb波動関数,
クーロン波動関数
英:
Coulomb wave function,仏:
Fonctions d'ondes de Coulomb,独:
Coulomb-wellenfunktion
2階の線形常微分方程式
は合流型超幾何微分方程式 (または Laguerre の陪微分方程式) の別表現であって、
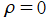
を確定特異点、
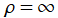
を1級の不確定特異点とする。これを Coulomb 波動方程式といい、その解の基本系
+b*G[l](η, ρ)](siki_spec230/coulomb00400.png)
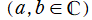
を成す二つの関数は、虚変数の
合流型超幾何関数
で表わせる。
](siki_spec230/coulomb00700.png)
および
](siki_spec230/coulomb00800.png)
を、第1種および第2種 Coulomb 波動関数という※1。ここに、
](siki_spec230/coulomb00700.png)
の複号はどちらを選択しても関数値は変わらない。また、
](siki_spec230/coulomb00900.png)
は Coulomb 正規化因子、
](siki_spec230/coulomb01000.png)
は Coulomb 位相シフト、
](siki_spec230/coulomb01100.png)
は単に (Coulomb 波動関数の) 位相と呼ばれ、
で定義される (グラフは
末尾の節を参照)。なお、

を 「Sommerfeld parameter」 と呼ぶことがある。
一般解の Coulomb 波動関数は
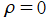
を対数分岐点とする無限多価関数で、分枝切断線を実軸上の区間
![(-∞, 0]](siki_spec230/coulomb01300.png)
に置く。
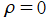
の近傍において、
](siki_spec230/coulomb00700.png)
は
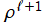
のごとく振る舞う。
](siki_spec230/coulomb00800.png)
は
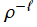
のごとく振る舞うが対数項
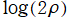
も含む。特に、
](siki_spec230/coulomb00700.png)
は
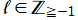
に限って超越整関数になり、
](siki_spec230/coulomb01800.png)
は

に関わらず常に超越整関数である。また、Coulomb 波動関数は
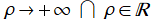
のときに、漸近近似式
に近付く。これは、
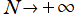
の漸近公式
において、
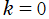
のみを取ると得られる。(導関数に対する漸近公式は、NISTの
33.11を参照。)
Coulomb 波動関数は、

に関して線形漸化式および微分漸化式
を満たす。ここに
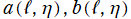
は、
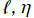
の二変数について1を周期とする任意の周期関数である。また、第1種と第2種の間で関係式
を満たす。
Coulomb 波動関数の積分表示式として、
等が知られている。(これは、後述の
Hankel - Coulomb 波動関数を示唆する。)
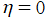
のとき、Coulomb 波動関数は
球 Bessel 関数
に還元される。
冒頭の定義式における合流型超幾何関数の部分は、
Whittaker 関数または
Laguerre 陪関数で書き換えることもできる。結局のところ、Coulomb 波動関数はこれらの関数と同クラスであるが、実変数で Bessel 関数的に振る舞う解として、後述する応用事例で特別に導入された。その理由もあって、Coulomb 波動関数の式は若干複雑である。
回転放物体座標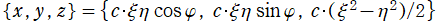
を用いて、Helmholtz 方程式
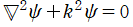
の解が
![ψ=Σ[m]Σ[h]{Ξ(ξ)Η(η)Φ(φ)}](siki_spec230/coulomb03300.png)
の形に変数分離されるとき、各座標方向は
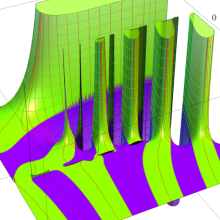
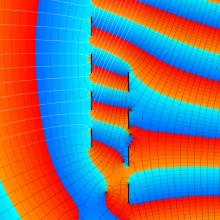
図:回転放物体座標における Helmholtz 方程式の解 (固有関数) →
Mathematica Code 
となり、
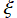
と

の方向に Coulomb 波動関数が現れる。ただし、この事実を物理学等へ応用した事例は、球座標や円柱座標の場合に比べるとずっと少ない。
むしろ、球座標を用いて Schrödinger 方程式を変数分離し、動径方向に現れる解を Coulomb 波動関数で記述した量子力学での事例が、この関数を導入する発端になったのであって、そこから派生した応用事例の方がより重要で数も多い。例えば、原子核の Rutherford 散乱および Coulomb 励起、水素原子内における電子の相対論的運動、Coulomb 斥力が働くポテンシャル障壁の透過性、
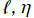
が複素数になる場合に拡張された原子核共鳴などが挙げられる※2。
Coulomb 波動関数の発端となった前述の事例について具体的に触れる。Coulomb ポテンシャル (原点からの距離
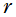
に反比例するポテンシャル) 下にある二つの荷電粒子が同符号の電荷
![Z[1], Z[2]](siki_spec230/coulomb03500.png)
を持つため、互いの間に Coulomb 斥力が働く (Coulomb 散乱状態と呼ばれる) 場合、その Schroedinger 方程式
を
球座標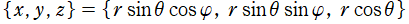
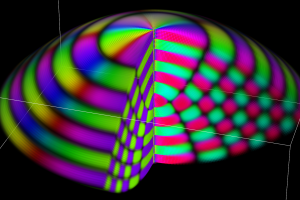
で変数分離すると、解
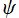
は
図:Coulomb 散乱状態の Schrödinger 方程式の解 (固有関数) →
Mathematica Code 
となり、
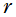
方向の解に第1種 Coulomb 波動関数が現れる (ただし
](siki_spec230/coulomb03900.png)
の正規化定数
![C[1]](siki_spec230/coulomb04000.png)
は任意とする)。すなわち、電荷の積
![Z[1]*Z[2]](siki_spec230/coulomb04100.png)
が正となるため、虚変数かつ複素次数の Laguerre 陪関数に相当する
](siki_spec230/coulomb00700.png)
が現れることになる※3。
【註記】
※1:NISTの
33.1によれば、
, G[l](η, ρ)](siki_spec230/coulomb04200.png)
を最初に導入したのは A. J. W. Sommerfeld (1928年) らしい。
なお、NISTの
33.14~33.21では、微分方程式
を満たす、別の型の Coulomb 波動関数
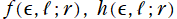
も掲載されている。ただし、この関数の各種公式は
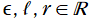
を前提としており、これを複素変数に拡張すると、互いの解析接続では延長できない複数の関数で定義域が区分されてしまう。よって、当サイトでは
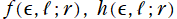
の詳細およびグラフは省略する。
※2:列挙した応用事例の内容と、20世紀前半という時期から推察されるとおり、Coulomb 波動関数は原子構造の解明および宇宙物理学への寄与のみならず、非常に悪い目的 ― 核兵器の開発 ― に使用されてしまう。
※3:もし、二粒子の電荷が異符号ならば
![Z[1]*Z[2]](siki_spec230/coulomb04100.png)
は負となり、互いの間に Coulomb 引力が働く。その場合は (水素原子の Schrödinger 方程式と本質的に同じ形になるので)
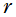
方向の解に Laguerre 陪関数が現れるが、これを※1 の
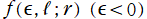
で書き換えることもできる。
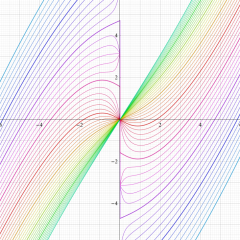
](siki_spec230/coulomb06400.png)

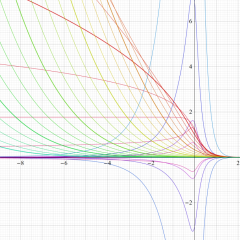
を実変数とする、第1種 Coulomb 波動関数のグラフ。
M. Abramowitz & I. Stegun 編 「Handbook of Mathematical Functions」 の541頁にあるものと同等または同様の図。

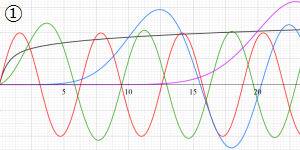
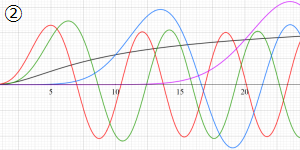
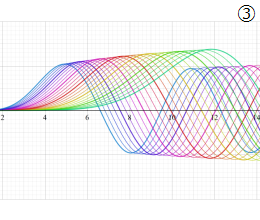
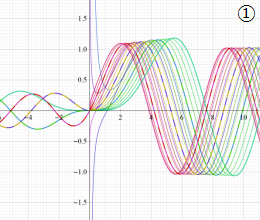
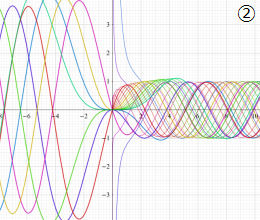
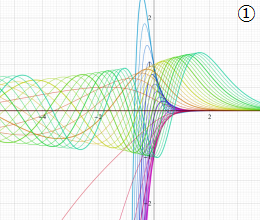
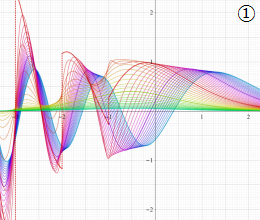
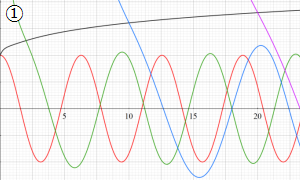
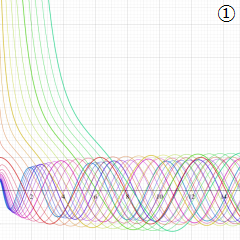
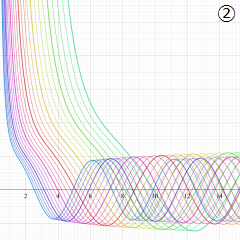
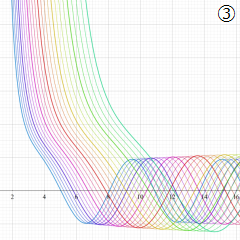
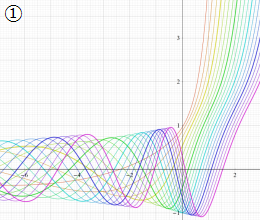
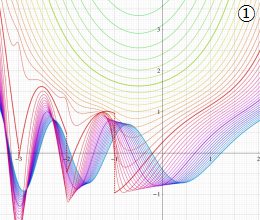
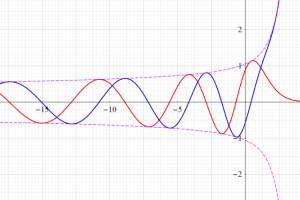
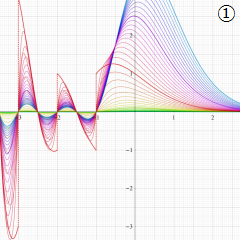
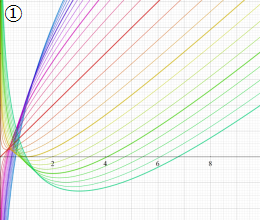
を実変数とする、第1種 Coulomb 波動関数のグラフ。①
](siki_spec230/coulomb04700.png)
, ②
](siki_spec230/coulomb04800.png)
, ③
](siki_spec230/coulomb04900.png)
。

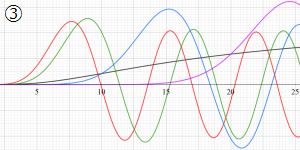
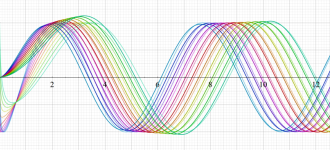
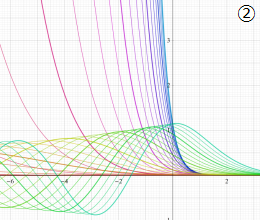
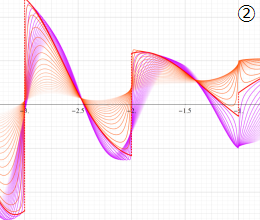
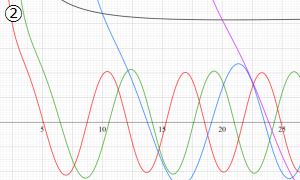
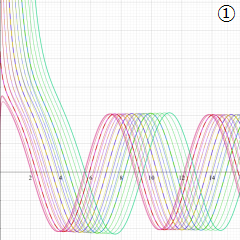
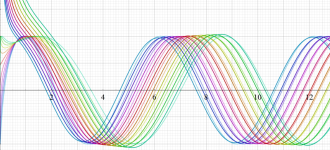
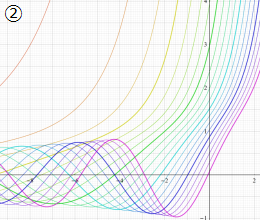
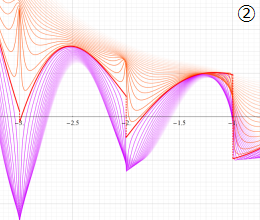
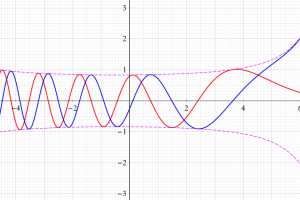
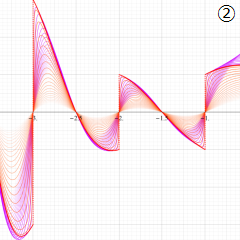
を実変数とする、第1種 Coulomb 波動関数のグラフ。①
](siki_spec230/coulomb05000.png)
, ②
](siki_spec230/coulomb05100.png)
。

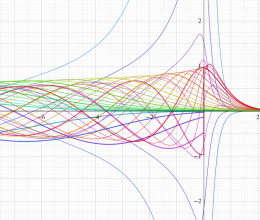
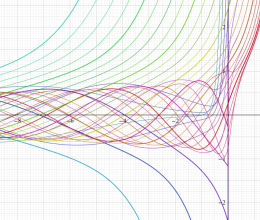
を実変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb00700.png)
のグラフは、
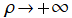
のとき
)](siki_spec230/coulomb05300.png)
に近付く。
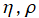
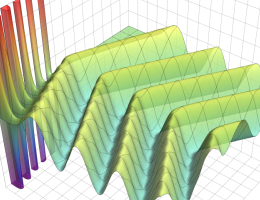
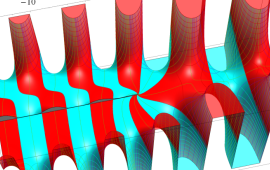
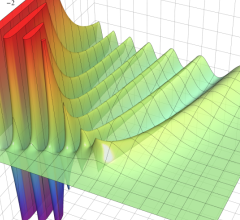
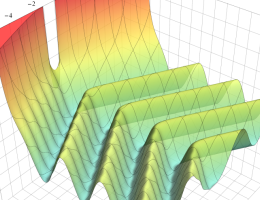
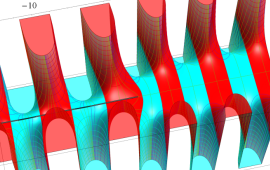
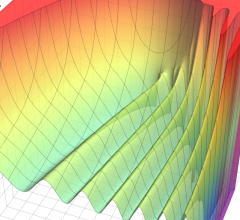
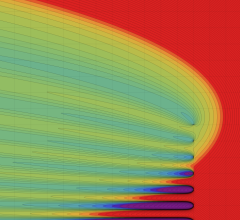
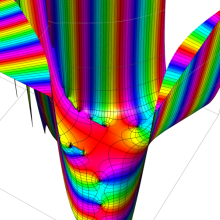
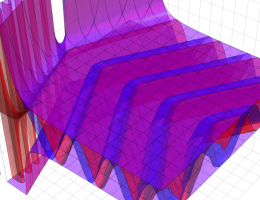
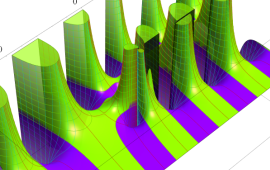
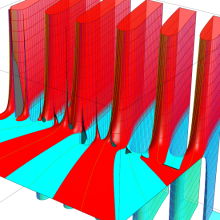
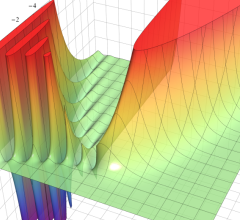
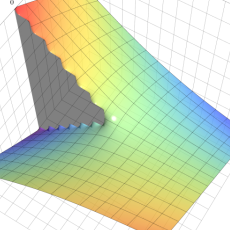
を実2変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb04700.png)
のグラフ。
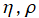
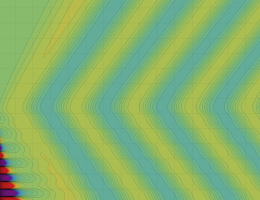
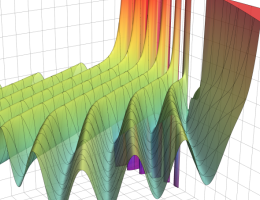
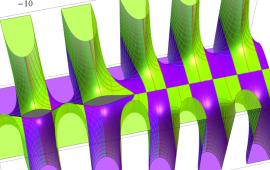
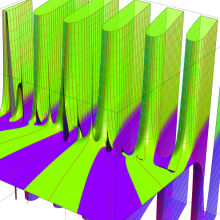
を実2変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb04800.png)
のグラフ。
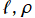
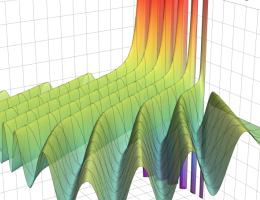
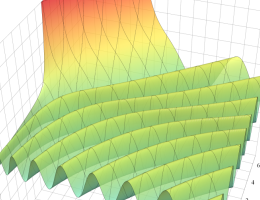
を実2変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb05000.png)
のグラフ。
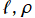
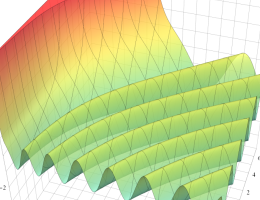
を実2変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb05100.png)
のグラフ。

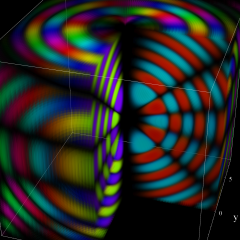
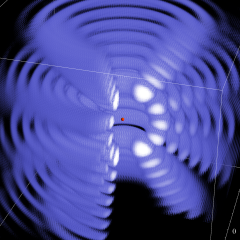
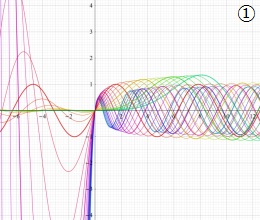
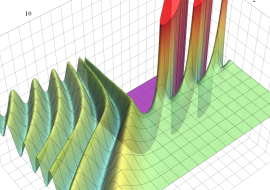
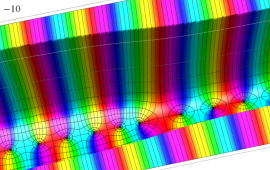
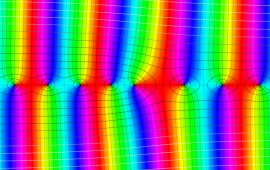
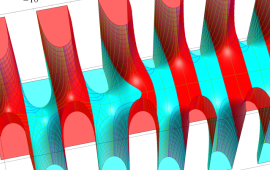
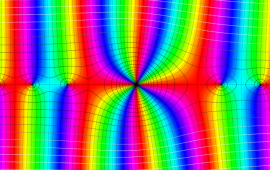
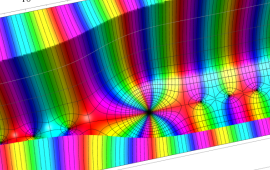
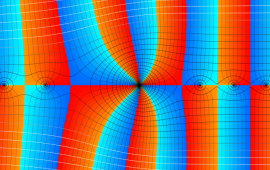
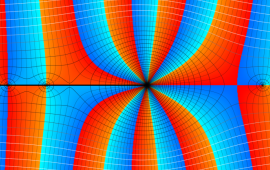
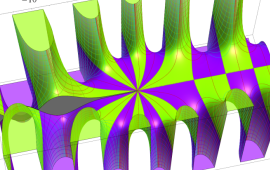
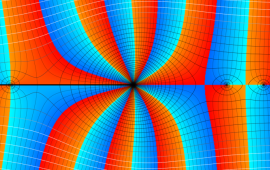
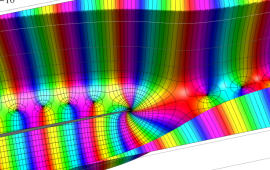
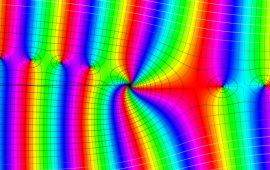
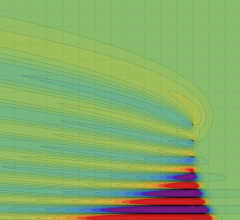
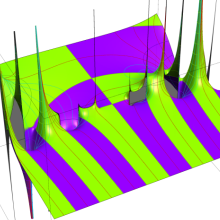
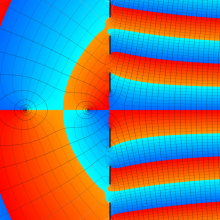
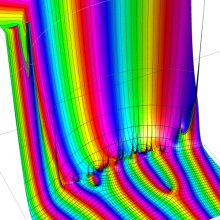
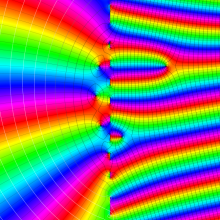
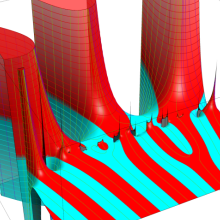
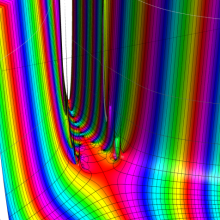
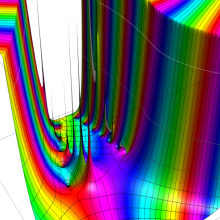
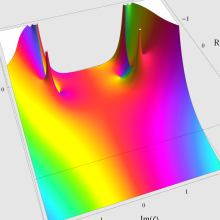
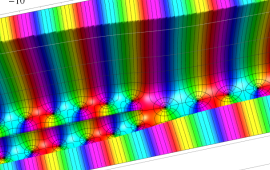
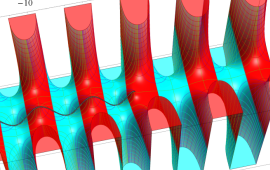
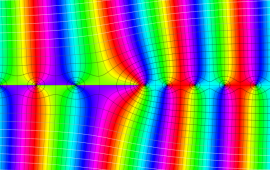
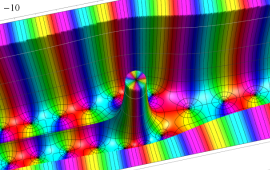
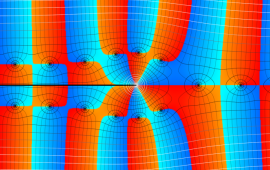
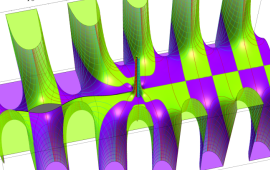
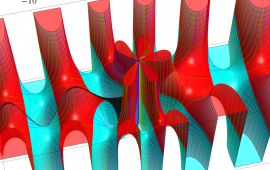
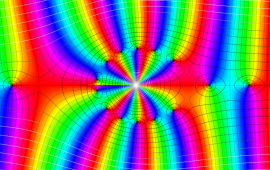
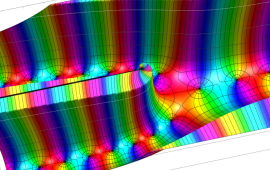
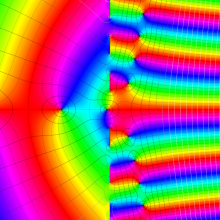
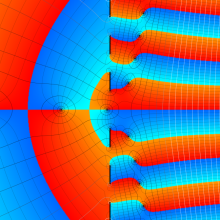
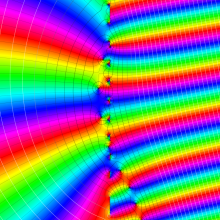
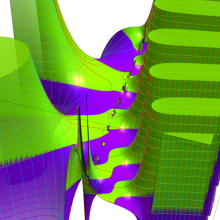
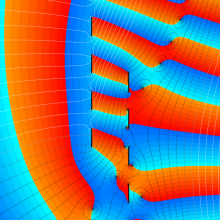
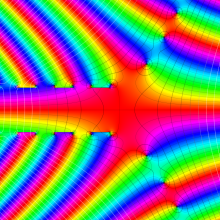
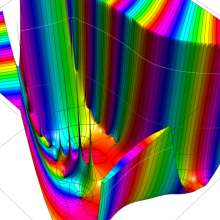
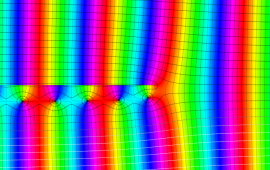
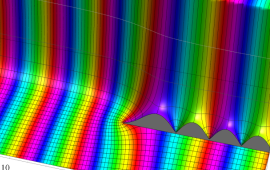
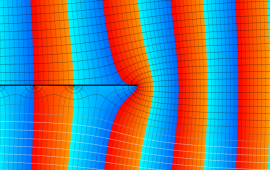
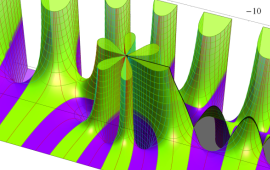
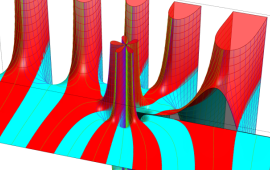
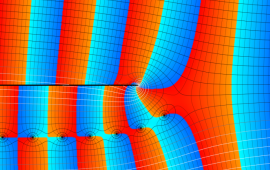
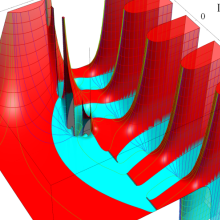
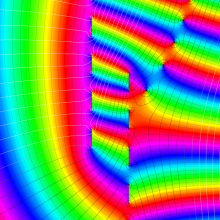
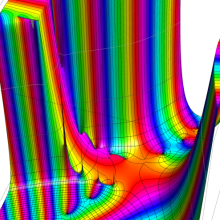
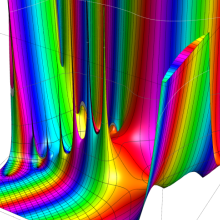
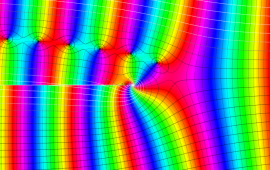
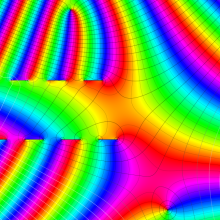
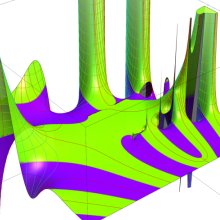
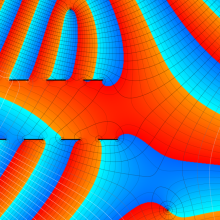
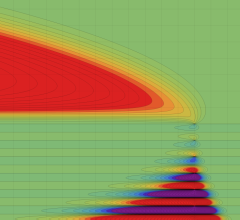
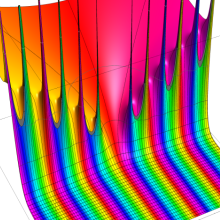
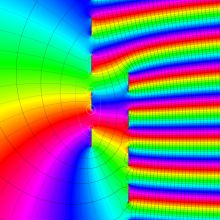
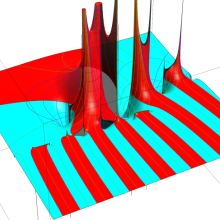
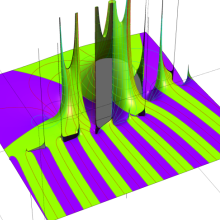
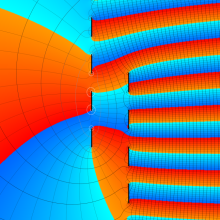
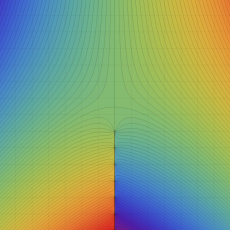
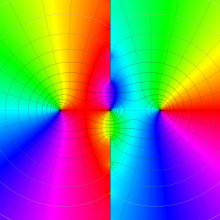
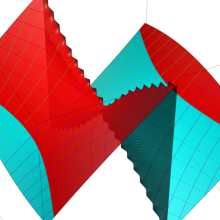
を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb05600.png)
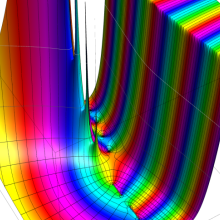
のグラフ。

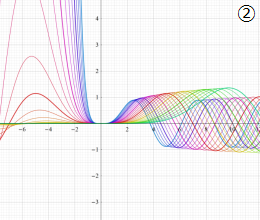
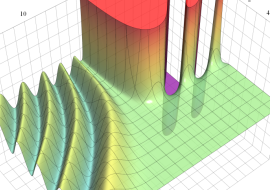
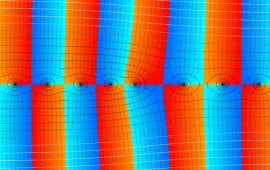
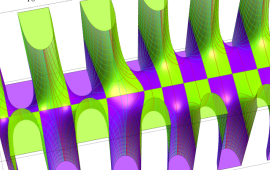
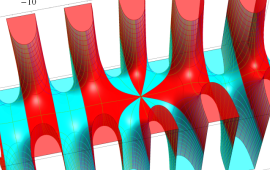
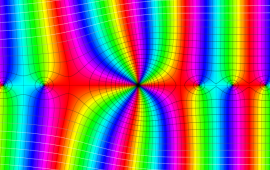
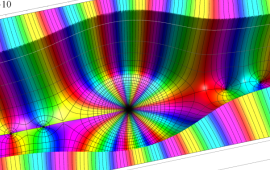
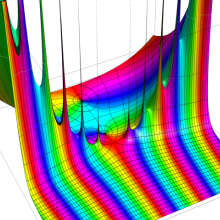
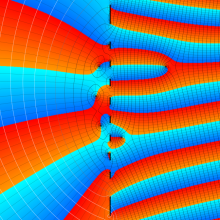
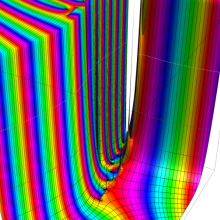
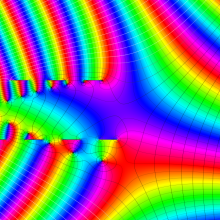
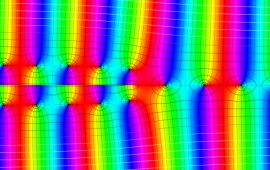
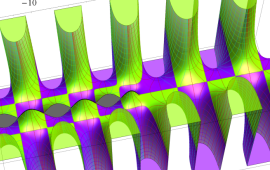
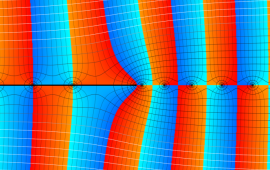
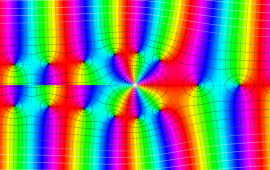
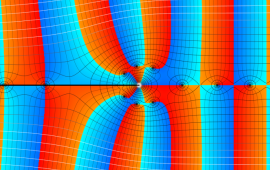
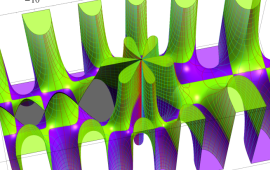
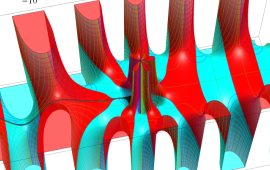
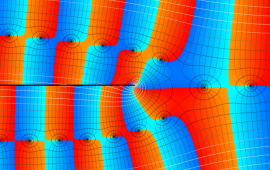
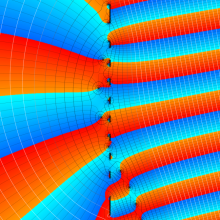
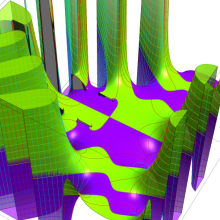
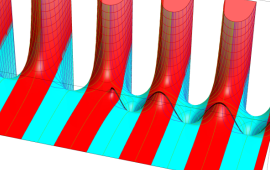
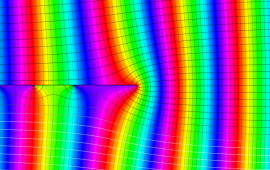
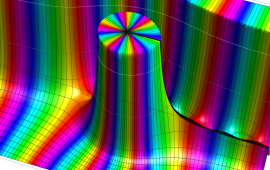
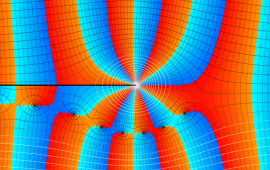
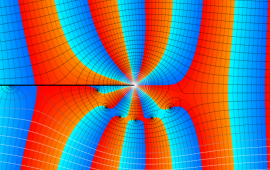
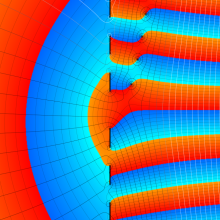
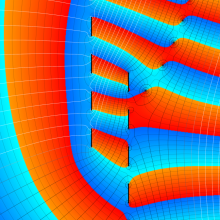
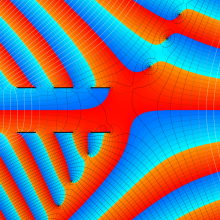
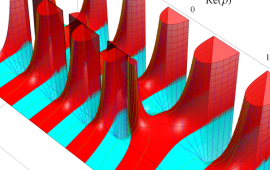
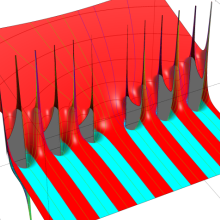
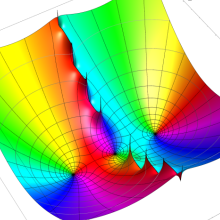
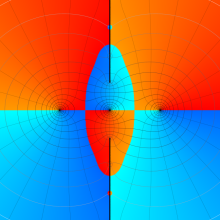
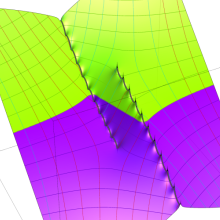
を複素変数とする、第1種 Coulomb 波動関数
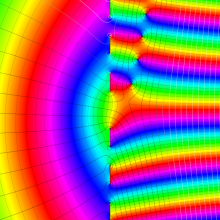
](siki_spec230/coulomb05700.png)
のグラフ。

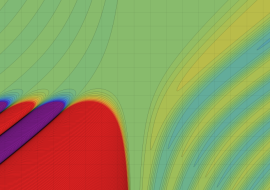
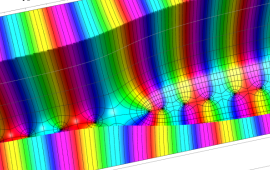
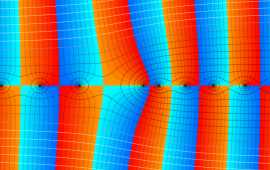
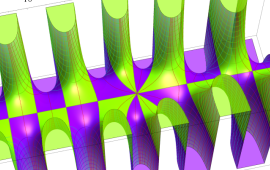
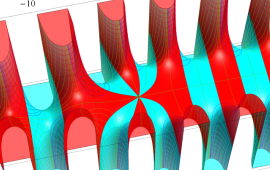
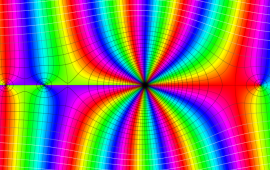
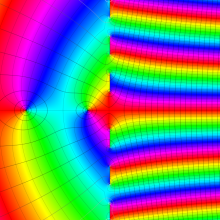
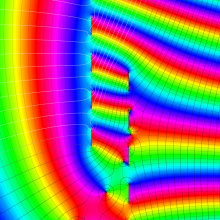
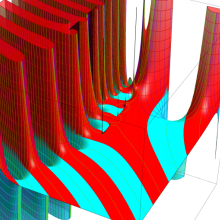
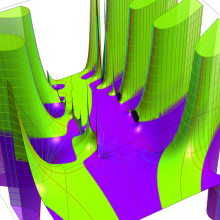
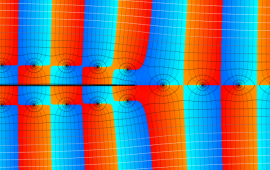
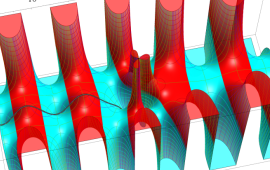
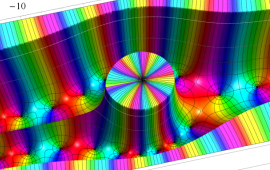
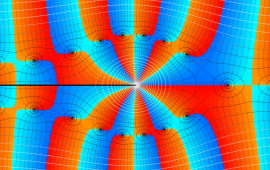
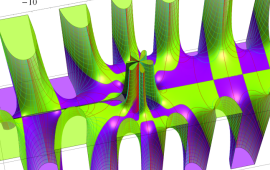
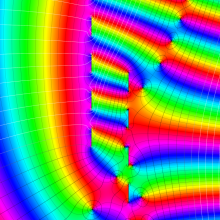
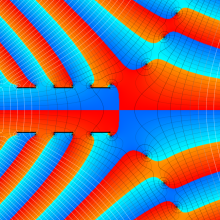
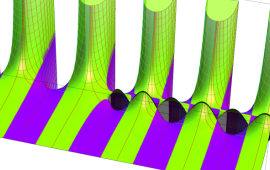
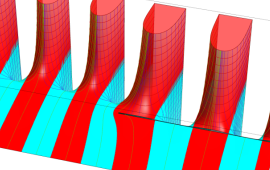
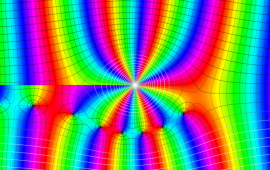
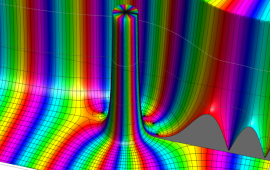
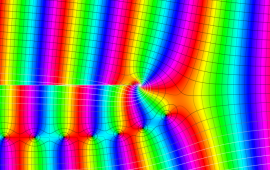
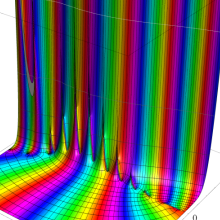
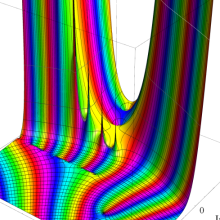
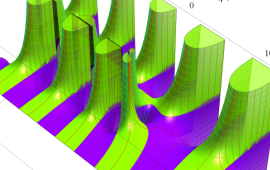
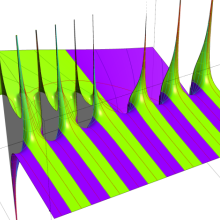
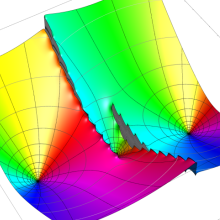
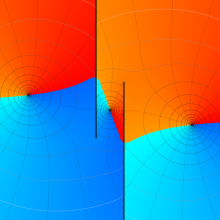
を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb05800.png)
のグラフ。

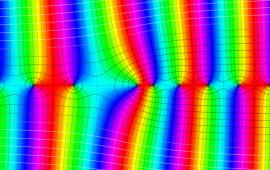
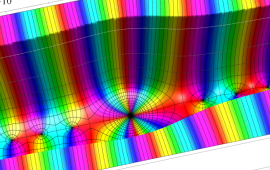
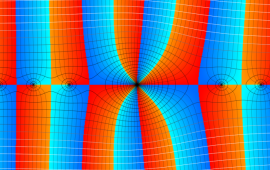
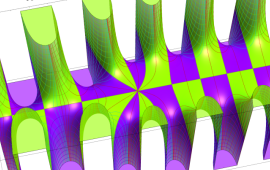
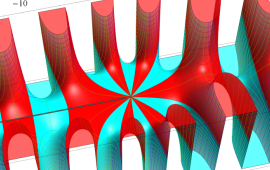
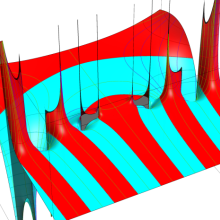
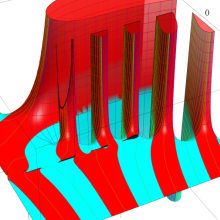
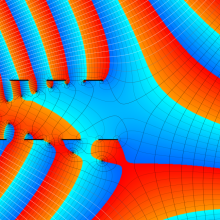
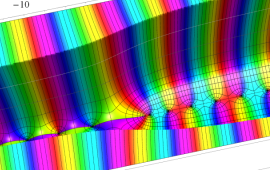
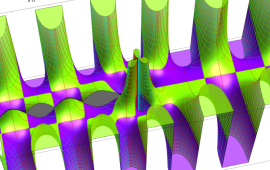
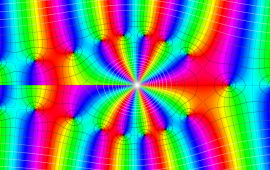
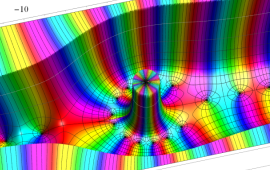
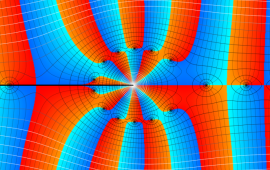
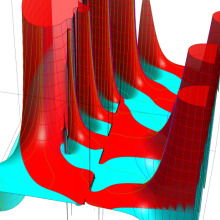
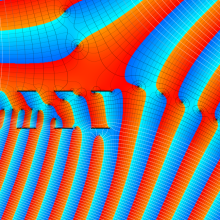
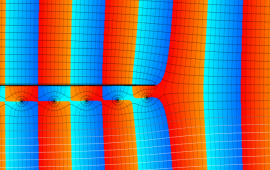
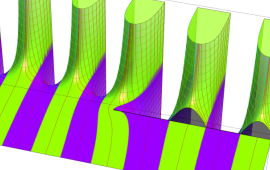
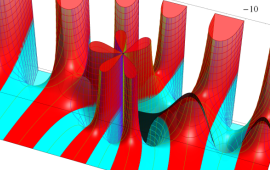
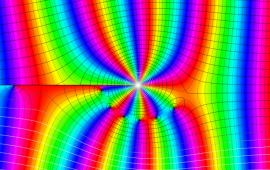
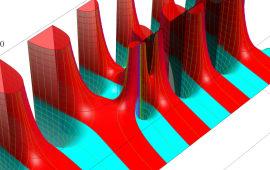
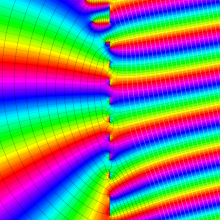
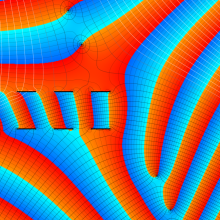
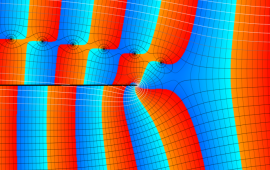
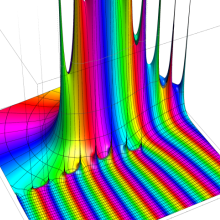
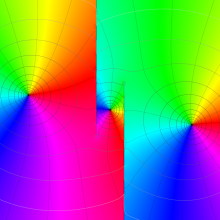
を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb05900.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06000.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06100.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06200.png)
のグラフ。
アニメーション
(8.38MB)

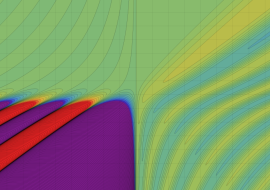
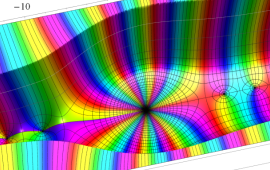
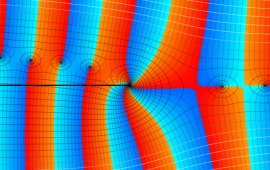
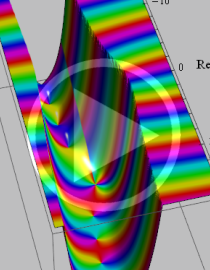
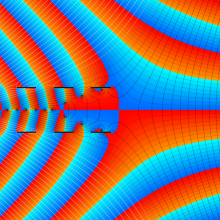
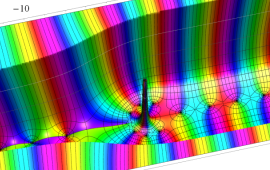
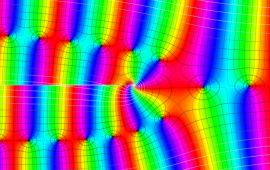
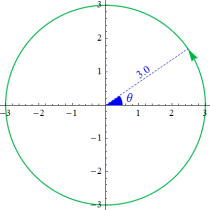
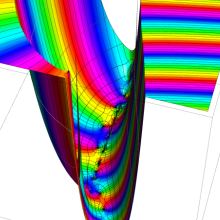
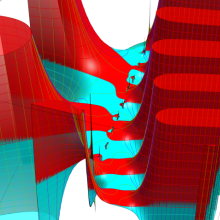
を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06300.png)
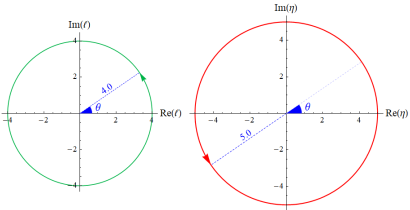
のグラフ。ただし複素数

は、2番目の図の経路に沿って動く。
 (変数η)](siki_spec230/coulomb06900.png)

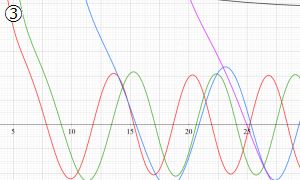
を実変数とする、第1種 Coulomb 波動関数のグラフ。①
](siki_spec230/coulomb04700.png)
, ②
](siki_spec230/coulomb04800.png)
。

を実変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06500.png)
のグラフ。
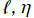
を実2変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06500.png)
のグラフ。

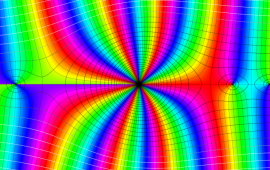
を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06600.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06700.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06800.png)
のグラフ。
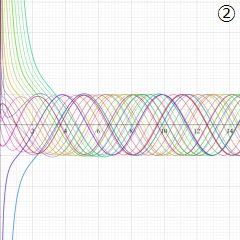
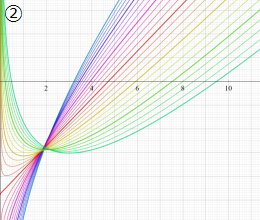
 (変数l)](siki_spec230/coulomb07500.png)

を実変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb06500.png)
のグラフ。
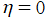
に限り、曲線は
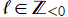
の位置で不連続になる。
②は、
](siki_spec230/coulomb06500.png)
の曲線が不連続になる
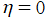
と、それに近い

を確認する。

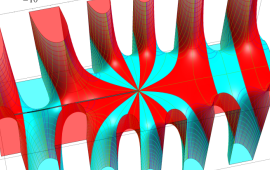
を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb07100.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb07200.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb07300.png)
のグラフ。
アニメーション
(12.7MB)

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb07400.png)
のグラフ。

を複素変数とする、第1種 Coulomb 波動関数
](siki_spec230/coulomb07450.png)
のグラフを、
Wikipedia に掲載されているそれ (2024年3月7日現在) と、ほぼ同じ体裁で描画する。(つまり、それは

を複素変数とするグラフではないことに注意する。)
](siki_spec230/coulomb09000.png)

を実変数とする、第2種 Coulomb 波動関数のグラフ。
M. Abramowitz & I. Stegun 編 「Handbook of Mathematical Functions」 の541頁にあるものと同等または同様の図。

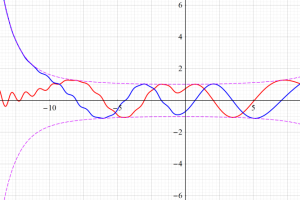
を実変数とする、第2種 Coulomb 波動関数のグラフ。①
](siki_spec230/coulomb07600.png)
, ②
](siki_spec230/coulomb07700.png)
, ③
](siki_spec230/coulomb07800.png)
。

を実変数とする、第2種 Coulomb 波動関数のグラフ。①
](siki_spec230/coulomb07900.png)
, ②
](siki_spec230/coulomb08000.png)
。

を実変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb00800.png)
のグラフは、
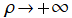
のとき
)](siki_spec230/coulomb08100.png)
に近付く。
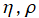
を実2変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb07600.png)
のグラフ。
を実2変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb07700.png)
のグラフ。
を実2変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb07900.png)
のグラフ。
を実2変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08000.png)
のグラフ。

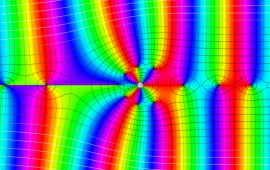
を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08200.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08300.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08400.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08500.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08600.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08700.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08800.png)
のグラフ。
アニメーション
(11.4MB)

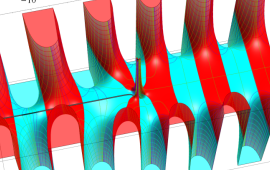
を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb08900.png)
のグラフ。ただし複素数

は、2番目の図の経路に沿って動く。
 (変数η)](siki_spec230/coulomb09500.png)

を実変数とする、第2種 Coulomb 波動関数のグラフ。①
](siki_spec230/coulomb07600.png)
, ②
](siki_spec230/coulomb07700.png)
。

を実変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09100.png)
のグラフ。
を実2変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09100.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09200.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09300.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09400.png)
のグラフ。
 (変数l)](siki_spec230/coulomb09900.png)

を実変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09100.png)
のグラフ。
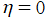
に限り、曲線は
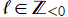
の位置で不連続になる。
②は、
](siki_spec230/coulomb09100.png)
の曲線が不連続になる
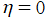
と、それに近い

を確認する。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09600.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09700.png)
のグラフ。

を複素変数とする、第2種 Coulomb 波動関数
](siki_spec230/coulomb09800.png)
のグラフ。
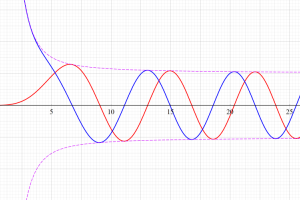
とG[l](η,ρ)の関係](siki_spec230/coulomb10200.png)
正弦・余弦関数に類似した
](siki_spec230/coulomb00700.png)
と
](siki_spec230/coulomb00800.png)
の関係。このとき、両者の包絡線は
=±Sqrt(F[l](η, ρ)^2+G[l](η, ρ)^2)](siki_spec230/coulomb10000.png)
となる。

が 0 に近いとき、

を実変数とする
](siki_spec230/coulomb00700.png)
と
](siki_spec230/coulomb00800.png)
のグラフは、負数方向で細かく振動する。しかし、
](siki_spec230/coulomb10100.png)
はそれでも振動しない ! 。
実2変数の
](siki_spec230/coulomb00700.png)
と
](siki_spec230/coulomb00800.png)
および
](siki_spec230/coulomb10100.png)
の関係。
Coulomb 波動方程式の二つの基本解は、原点での振る舞いに着目して選ぶと
, G[l](η, ρ)](siki_spec230/coulomb04200.png)
となるが、無限遠点での振る舞いに着目すると、
Hankel 関数に類似した定義
を選ぶことになる。つまり、一般解を
+b*H2[l](η, ρ)](siki_spec230/coulomb10400.png)
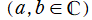
と表記しても良い。
](siki_spec230/coulomb10500.png)
および
](siki_spec230/coulomb10600.png)
を、第1種および第2種 Hankel - Coulomb 波動関数という※1。結局のところ、
, H2[l](η, ρ)](siki_spec230/coulomb10700.png)
の表示式や性質の多くは上記の定義式から導かれるが、以下ではその幾つかについて具体的に触れる。
Hankel - Coulomb 波動関数は、虚変数の合流型超幾何関数
で表わせる。ここに、
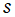
および
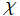
は
前節で述べた式と同じである。
第1種・第2種ともに、Hankel - Coulomb 波動関数は
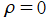
を対数分岐点とする無限多価関数で、分枝切断線を実軸上の区間
![(-∞, 0]](siki_spec230/coulomb01300.png)
に置く。また、両者は
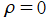
の近傍において対数項
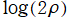
を含む形で振る舞う。
Hankel - Coulomb 波動関数は
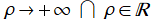
のときに、漸近近似式
に近付く。これも、
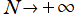
の漸近公式
において、
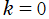
のみを取ると得られる。ここに、
![f[k]](siki_spec230/coulomb11100.png)
および
![g[k]](siki_spec230/coulomb11200.png)
は前節の式と全く同じである。
Hankel - Coulomb 波動関数は、Coulomb 波動関数と全く同じ形の、

に関する線形漸化式および微分漸化式を満たす。また、第1種と第2種の間または
](siki_spec230/coulomb00700.png)
との間で、関係式
を満たす。
前節での示唆によれば、Hankel - Coulomb 波動関数の積分表示式は、
となることが容易に分かる。
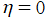
のとき、Hankel - Coulomb 波動関数は
球 Hankel 関数
に還元される。
応用または数値計算において、Hankel - Coulomb 波動関数は Coulomb 波動関数とともに現れるが、特に、前節の球座標で変数分離したときの問題における動径方向の解を、
](siki_spec230/coulomb10500.png)
は中心に向かう球面波として、
](siki_spec230/coulomb10600.png)
は外部に向かう球面波として表わす応用事例がある。
【註記】
※1:Coulomb - Hankel 関数と呼ぶこともある。
](siki_spec230/coulomb12100.png)

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb11600.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb11700.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb11800.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb11900.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12000.png)
のグラフ。
 (変数η)](siki_spec230/coulomb12500.png)

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12200.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12300.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12400.png)
のグラフ。
 (変数l)](siki_spec230/coulomb12900.png)

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12600.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12700.png)
のグラフ。

を複素変数とする、第1種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb12800.png)
のグラフ。
](siki_spec230/coulomb13100.png)

を複素変数とする、第2種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb13000.png)
のグラフ。
アニメーション
(11.2MB)

を複素変数とする、第2種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb10600.png)
のグラフ。ただし複素数
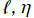
は、2番目の図の経路に沿って動く。
 (変数η)](siki_spec230/coulomb13300.png)

を複素変数とする、第2種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb13200.png)
のグラフ。
 (変数l)](siki_spec230/coulomb13600.png)

を複素変数とする、第2種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb13400.png)
のグラフ。

を複素変数とする、第2種 Hankel - Coulomb 波動関数
](siki_spec230/coulomb13500.png)
のグラフ。
以下では、既に
冒頭で説明した Coulomb 正規化因子
](siki_spec230/coulomb00900.png)
、Coulomb 位相シフト
](siki_spec230/coulomb01000.png)
、および位相
](siki_spec230/coulomb01100.png)
のグラフを参考までに掲載する。ただし、これらは本質的に
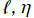
の
対数ガンマ関数、および

の対数関数であるから、掲載数は最小限に留める。
](siki_spec230/coulomb13900.png)

を実変数とする、Coulomb 正規化因子
](siki_spec230/coulomb00900.png)
のグラフ。

を実変数とする、Coulomb 正規化因子
](siki_spec230/coulomb00900.png)
のグラフ。
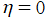
に限り、曲線は
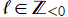
の位置で不連続になる。
②は、
](siki_spec230/coulomb00900.png)
の曲線が不連続になる
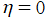
と、それに近い

を確認する。
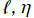
を実2変数とする、Coulomb 正規化因子
](siki_spec230/coulomb00900.png)
のグラフ。

を複素変数とする、Coulomb 正規化因子
](siki_spec230/coulomb13700.png)
のグラフ。

を複素変数とする、Coulomb 正規化因子
](siki_spec230/coulomb13800.png)
のグラフ。
](siki_spec230/coulomb14200.png)

を実変数とする、Coulomb 位相シフト
](siki_spec230/coulomb01000.png)
のグラフ。
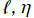
を実2変数とする、Coulomb 位相シフト
](siki_spec230/coulomb01000.png)
のグラフ。

を複素変数とする、Coulomb 位相シフト
](siki_spec230/coulomb14000.png)
のグラフ。

を複素変数とする、Coulomb 位相シフト
](siki_spec230/coulomb14100.png)
のグラフ。
](siki_spec230/coulomb14500.png)
Coulomb 波動関数の位相
](siki_spec230/coulomb01100.png)
は、

について初等関数 (一次関数+対数関数) であり、
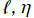
についても "一次関数+
](siki_spec230/coulomb01000.png)
" の形になっている。よって、

を実変数とする
](siki_spec230/coulomb01100.png)
のグラフのみを掲載する。

を実変数とする、Coulomb 波動関数の位相のグラフ。①
](siki_spec230/coulomb14300.png)
, ②
](siki_spec230/coulomb14400.png)
。
, G[l](η, ρ)](siki_spec230/coulomb04200.png) を最初に導入したのは A. J. W. Sommerfeld (1928年) らしい。
を最初に導入したのは A. J. W. Sommerfeld (1928年) らしい。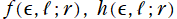 も掲載されている。ただし、この関数の各種公式は
も掲載されている。ただし、この関数の各種公式は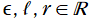 を前提としており、これを複素変数に拡張すると、互いの解析接続では延長できない複数の関数で定義域が区分されてしまう。よって、当サイトでは
を前提としており、これを複素変数に拡張すると、互いの解析接続では延長できない複数の関数で定義域が区分されてしまう。よって、当サイトでは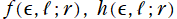 の詳細およびグラフは省略する。
の詳細およびグラフは省略する。![Z[1]*Z[2]](siki_spec230/coulomb04100.png) は負となり、互いの間に Coulomb 引力が働く。その場合は (水素原子の Schrödinger 方程式と本質的に同じ形になるので)
は負となり、互いの間に Coulomb 引力が働く。その場合は (水素原子の Schrödinger 方程式と本質的に同じ形になるので)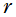 方向の解に Laguerre 陪関数が現れるが、これを※1 の
方向の解に Laguerre 陪関数が現れるが、これを※1 の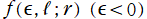 で書き換えることもできる。
で書き換えることもできる。