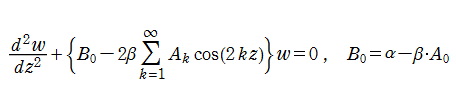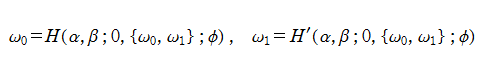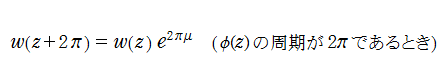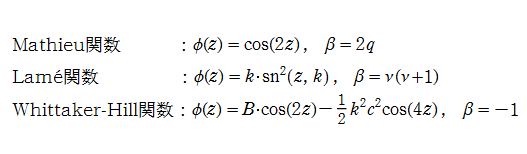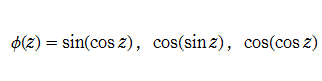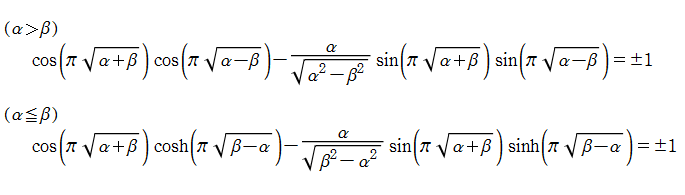特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
特殊関数 Menu
Hill 関数
Hill 関数 (周期関数項が楕円テータ関数)
日:Hill関数,ヒル関数英:Hill function,仏:Fonction de Hill,独:Hillsche funktion
2階の線形常微分方程式
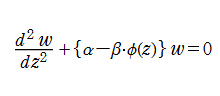
天体力学における制限三体問題(3天体のうち、2天体は互いの重心を楕円軌道で公転し、残り1天体の質量が他に比べて無視できるほど小さい場合の1天体の軌道)の理想的な周期軌道解を求めるため、1886年に G. W. Hill がこの微分方程式を考察した。
の形でも定義される。Hill の微分方程式の解
は初期値である※1。
Hill の微分方程式は周期関数項を持つ基本的な線形常微分方程式とみなされる。
なる擬周期性を満たすように選ぶことができる。これは Floquet の定理と呼ばれ、このときの
Hill 関数の特別な場合としては、
等がある。Mathieu 関数,Lamé 関数については、それぞれ個別の頁で既に触れているので、ここでは扱わない。また、Whittaker - Hill 関数のグラフの概形は Mathieu 関数とよく似ているので、これも省略する※2。
そこで、この頁では順に
を扱うことにする。ただし、Mathieu 関数や Lamé 関数のときのように、Floquet の定理に基づいて、基本解の一方が周期関数となる特別な場合を選んでグラフを描画することは(難しいため)しない。代わりに、初期値の設定によって偶関数と奇関数になる二つの場合をもって基本解の代表とする。
【註記】
※1 Hill 関数の標準的な関数記号はまだ存在しないため、便宜的にこのような表記にした。なお、以降ではこの関数記号の末尾引数における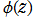 を、#と&で表現している。これはプログラミング構文における 「純関数」 または 「ラムダ計算」 の記述方法に相当する。
を、#と&で表現している。これはプログラミング構文における 「純関数」 または 「ラムダ計算」 の記述方法に相当する。
※2 複素変数の Whittaker - Hill 関数も、「NDSolveHill.m」 にある関数 ”Hill[ ]” を用いて計算できます。
※1 Hill 関数の標準的な関数記号はまだ存在しないため、便宜的にこのような表記にした。なお、以降ではこの関数記号の末尾引数における
※2 複素変数の Whittaker - Hill 関数も、「NDSolveHill.m」 にある関数 ”Hill[ ]” を用いて計算できます。
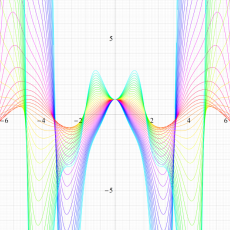
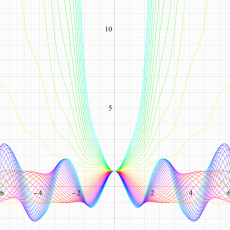
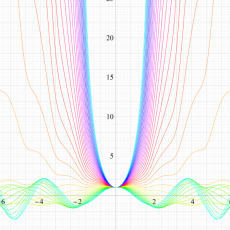
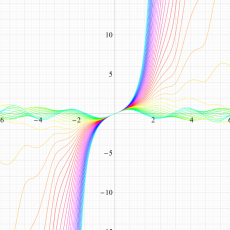
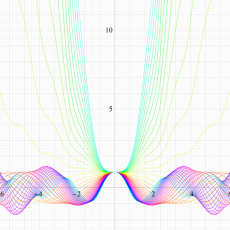
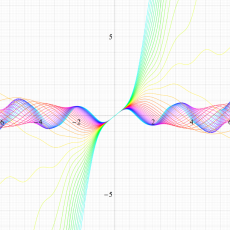
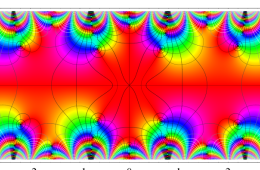
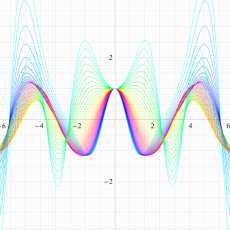
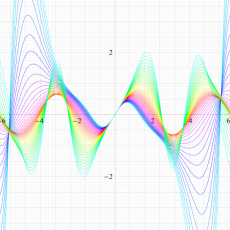
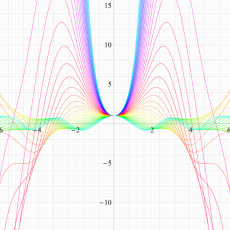
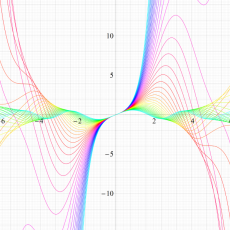
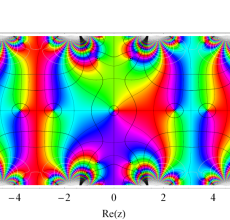
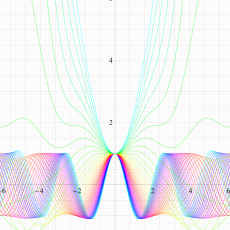
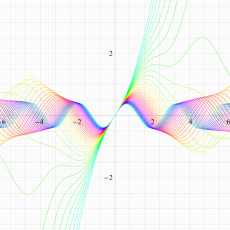
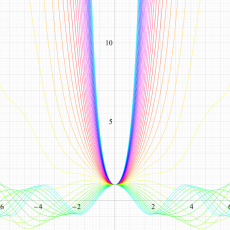
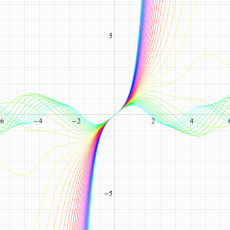
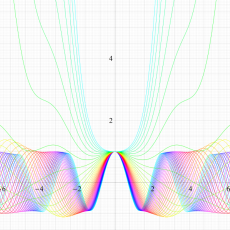
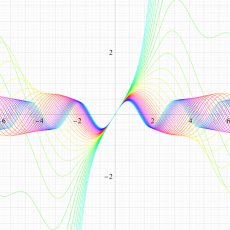
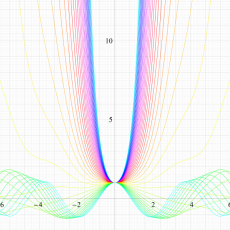
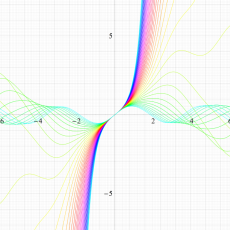
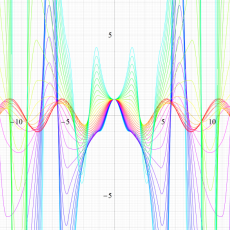
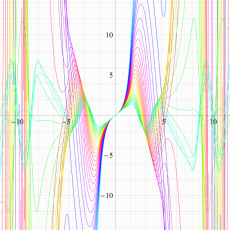
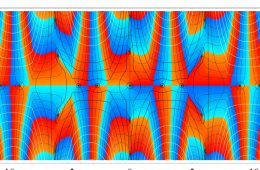
実変数の Hill 関数のグラフ。順に、①
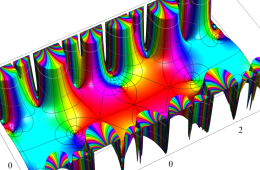
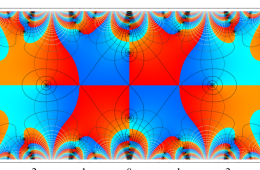
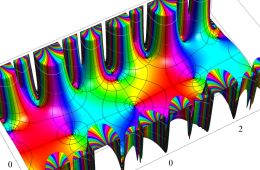
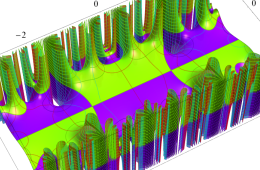
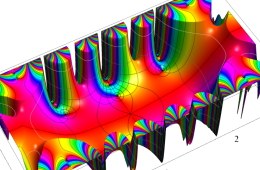
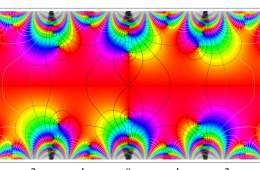
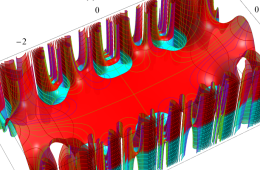
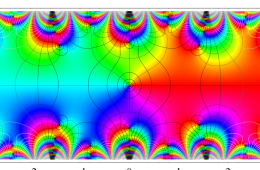
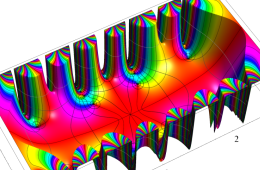
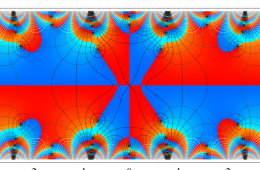
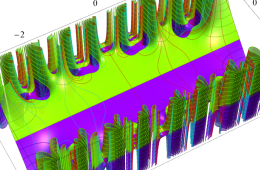
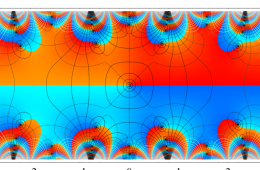
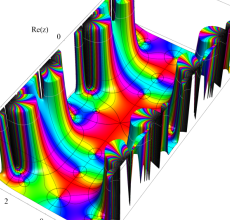
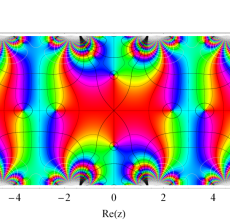
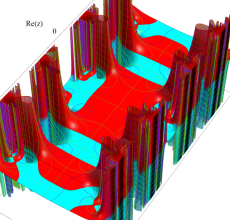
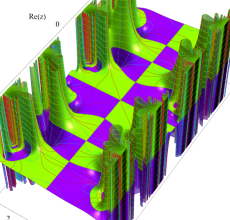
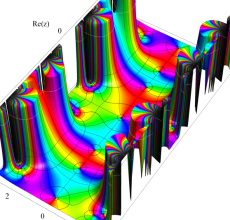
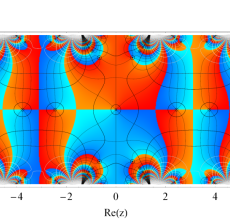
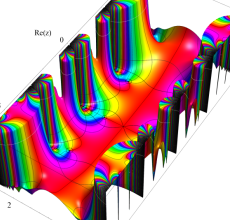
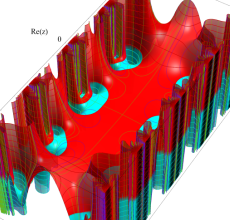
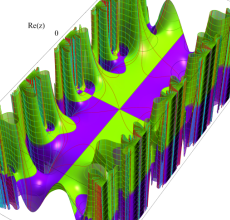
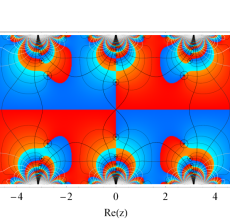
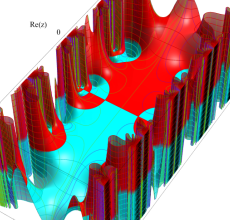
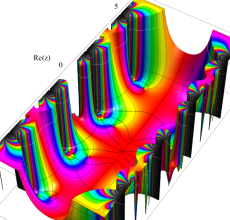
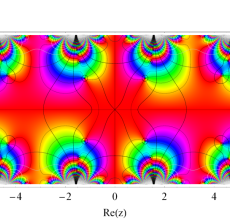
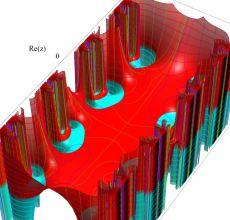
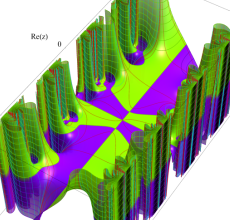
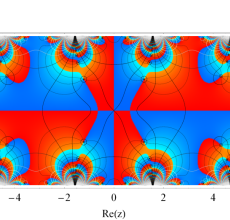
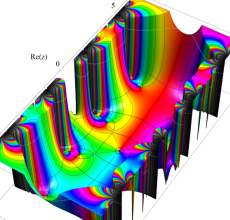
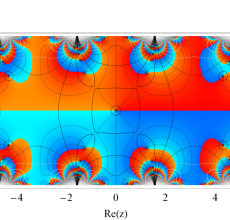
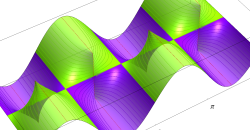
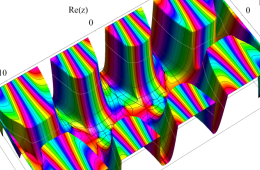
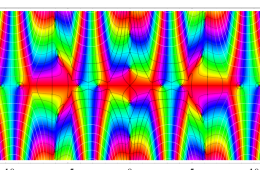
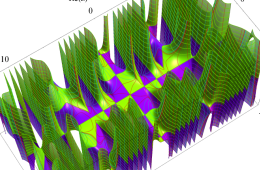
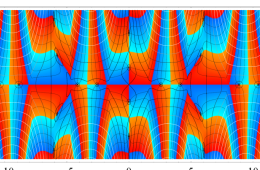
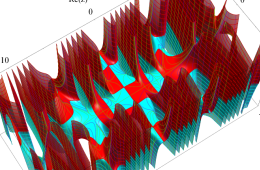
複素変数の Hill 関数
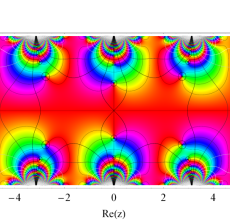
複素変数の Hill 関数
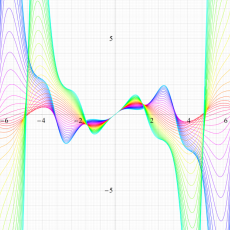
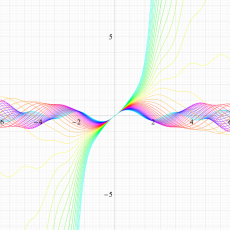
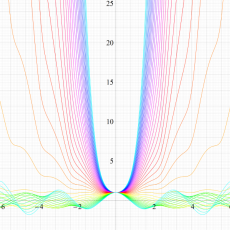
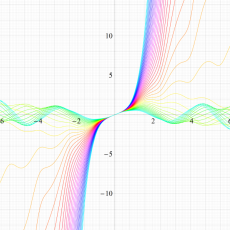
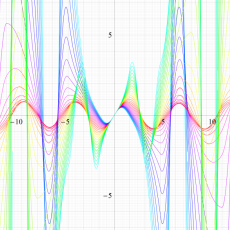
実変数の Hill 関数のグラフ。順に、①
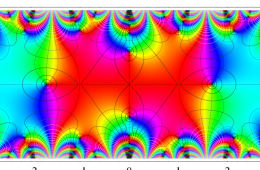
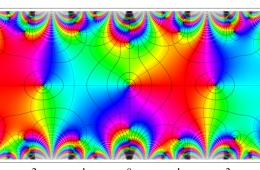
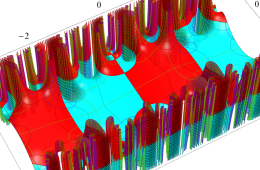
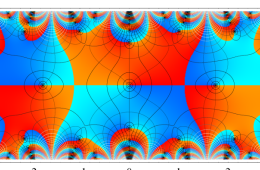
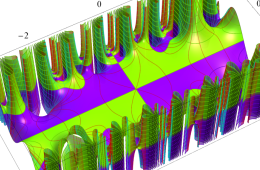
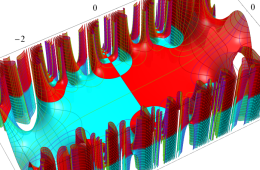
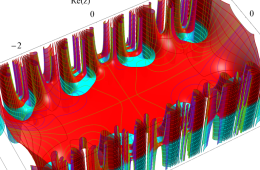
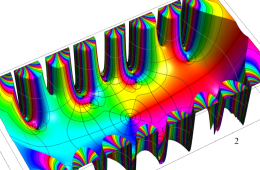
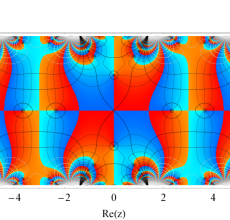
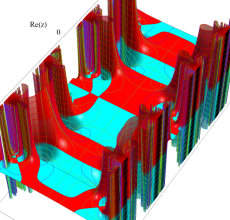
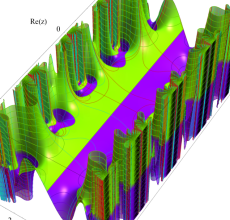
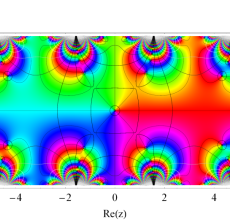
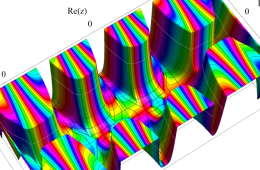
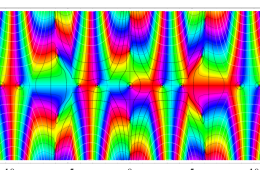
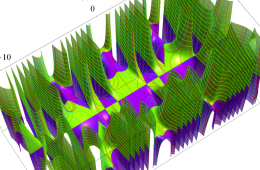
複素変数の Hill 関数
複素変数の Hill 関数
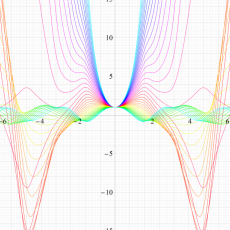
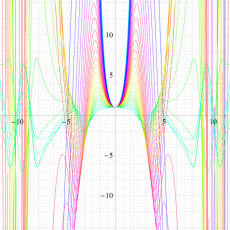
実変数の Hill 関数のグラフ。順に、①
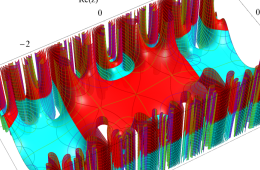
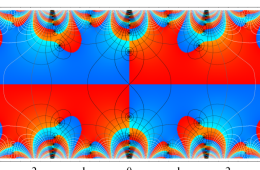
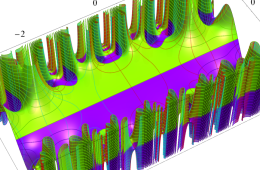
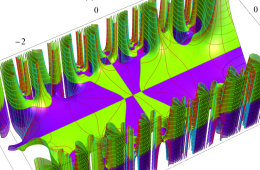
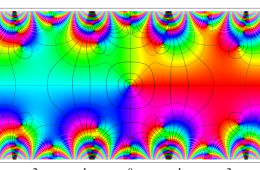
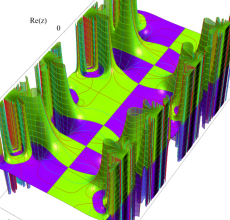
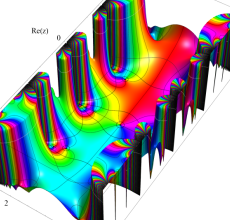
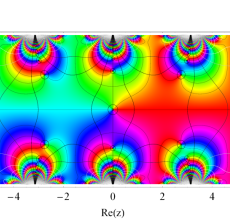
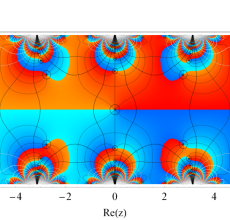
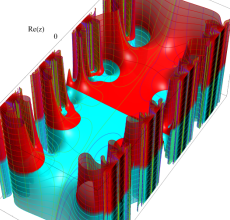
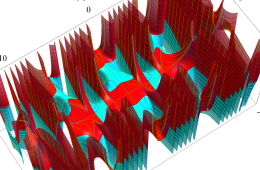
複素変数の Hill 関数
複素変数の Hill 関数
Hill 関数 (周期関数項が合成三角関数)
ここでは特に、Hill の微分方程式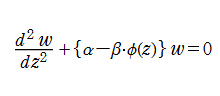
となる場合について考察する。
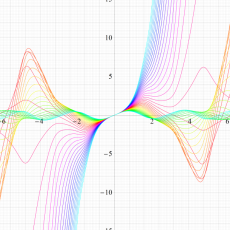
実変数の Hill 関数のグラフ。順に、①
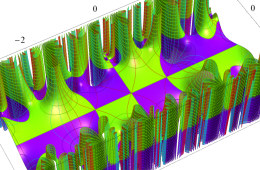
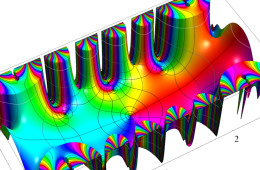
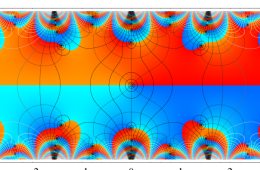
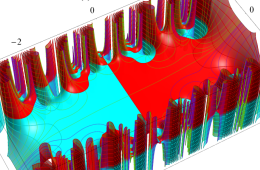
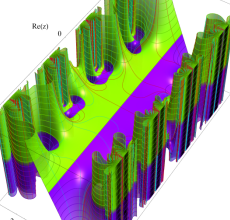
複素変数の Hill 関数
複素変数の Hill 関数
実変数の Hill 関数のグラフ。順に、①
複素変数の Hill 関数
複素変数の Hill 関数
実変数の Hill 関数のグラフ。順に、①
複素変数の Hill 関数
複素変数の Hill 関数
Meissner 関数
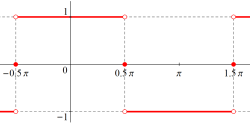
ここでは特に、Hill の微分方程式における周期関数項が矩形波関数※1となった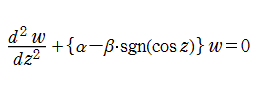
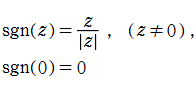
また、
で表わされる。
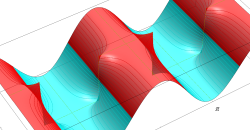
実変数の Meissner 関数のグラフ。順に、①
複素変数の Meissner 関数
複素変数の Meissner 関数