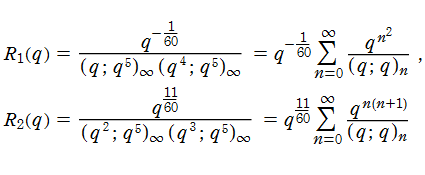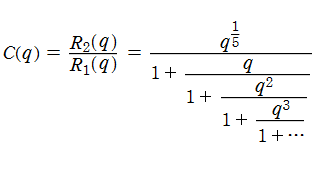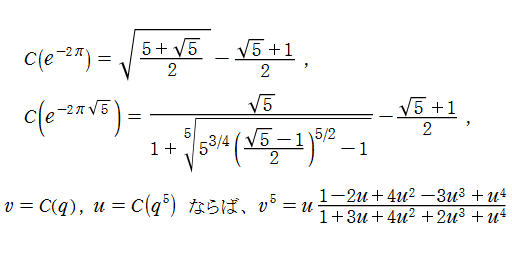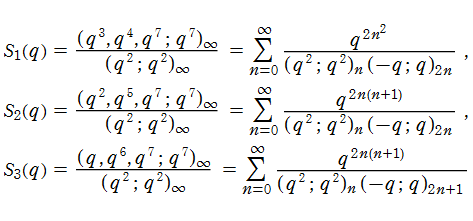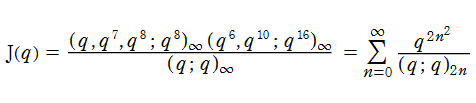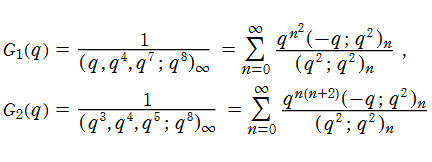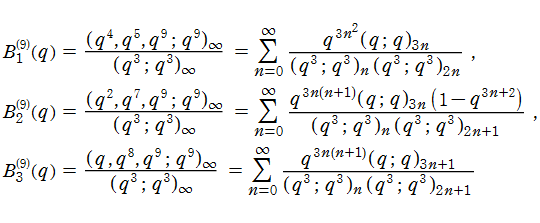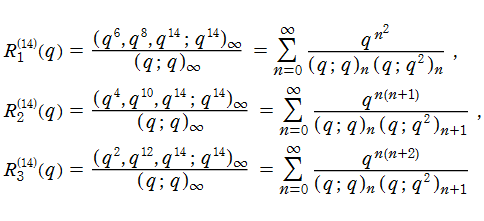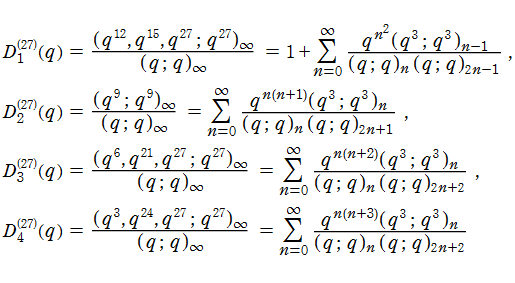特殊関数 グラフィックスライブラリー
Graphics Library of Special functions

その他のq-級数

Rogers - Ramanujan 恒等式

日：Rogers - Ramanujan恒等式，ロジャース - ラマヌジャン恒等式
英：Rogers-Ramanujan identities，仏：Identités de Rogers-Ramanujan，独：Rogers-Ramanujan-Identitäten

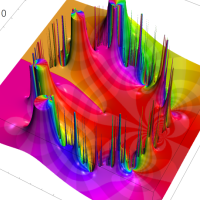
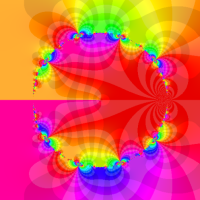
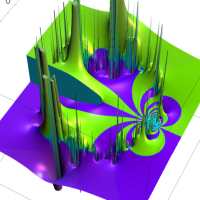
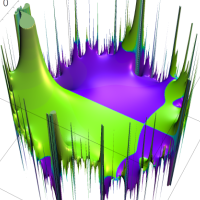
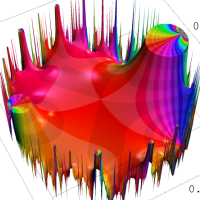
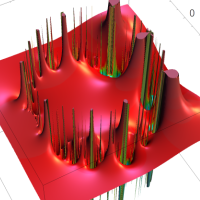
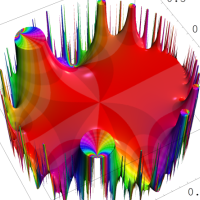
　この頁では、q-解析学でよく現れる無限乗積と無限級数との関係を表わす恒等式を、関数として見るとともに複素領域でグラフ描画する。
　これらの恒等式は、L. Euler による五角数に関連する q-級数 (→ Dedekind のエータ関数) と、C. G. J. Jacobi によるその簡易な証明法とを起源とするが、現在では他にもおびただしい種類の恒等式が発見されている。それらは主に、q-一般超幾何関数の特殊値として導びかれる。そのほとんどは一見して非自明な恒等式であり、多くの人々が「美しい数式」と評することで知られる。
　数論、組み合わせ論での応用がほとんどであるが、中には超弦理論などの物理学に現れるものもある。
　Rogers - Ramanujan 恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。(因子を除く場合が多いが、ここでは上記の式を採用する。)
　また、この二つの級数の商は、連分数によって

• 

と表わされる。これを特に、Rogers - Ramanujan の連分数という。
　この恒等式は、1894年に L. J. Rogers が初めて証明し、独立に S. Ramanujan によっても発見されたものである。さらに、Ramanujan はの性質として、

• 

を主張した。これらは後に、Rogers 等が証明を与えた。
　統計力学における三角形格子上の粒子模型 (Hard Hexagon Model) では、粒子の局所状態密度を表わす解を求めると Rogers - Ramanujan 恒等式 (の q-級数) が現れることを、1980年に R. J. Baxter が示した。

　複素変数の Rogers - Ramanujan 恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Rogers - Ramanujan 恒等式のグラフ。

• 
• 
• 
• 
• 

　実変数の Rogers - Ramanujan 連分数のグラフ。

• 

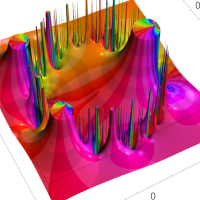
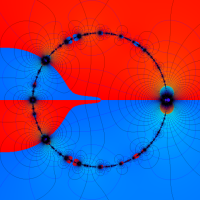
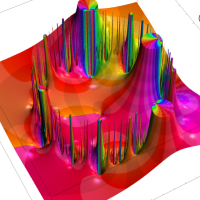
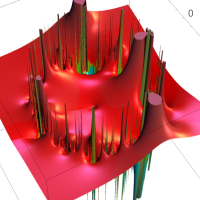
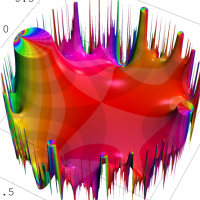
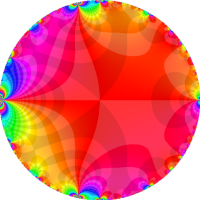
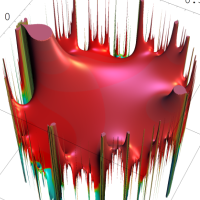
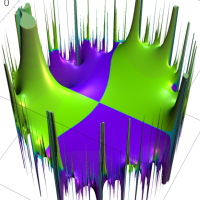
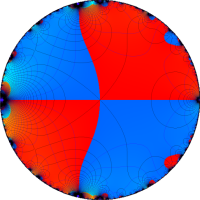
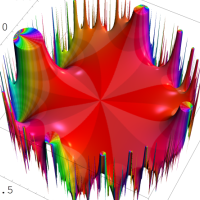
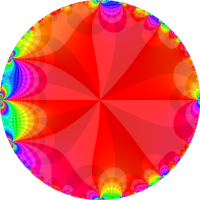
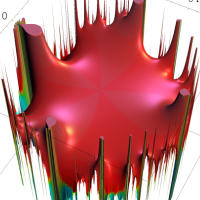
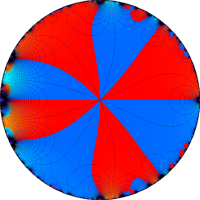
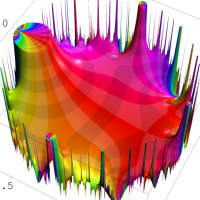
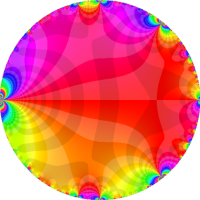
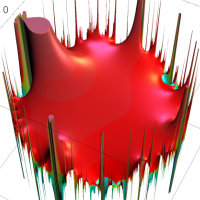
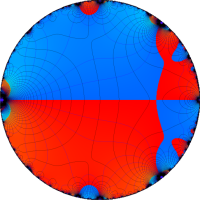
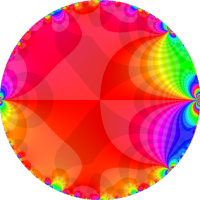
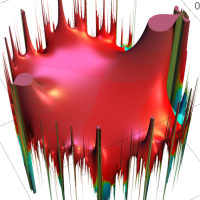
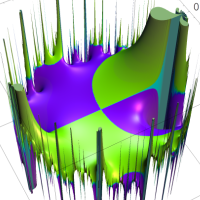
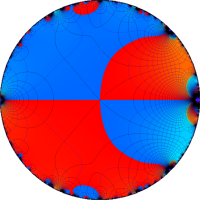
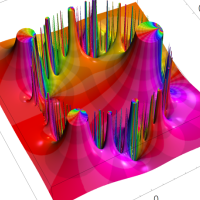
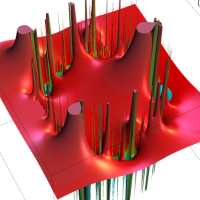
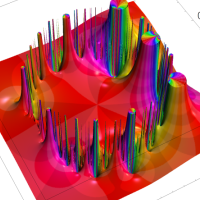
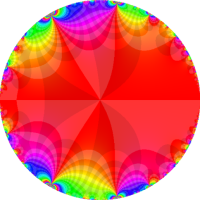
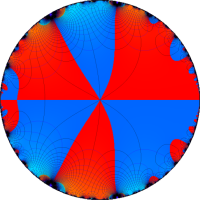
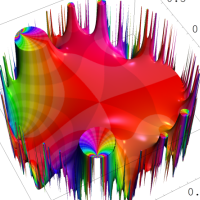
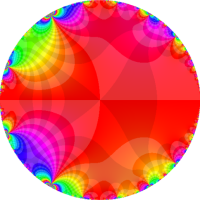
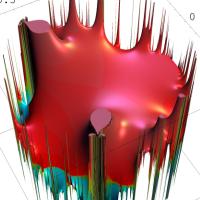
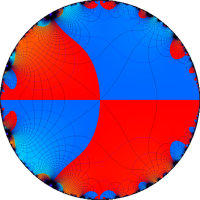
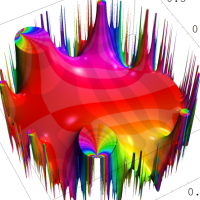
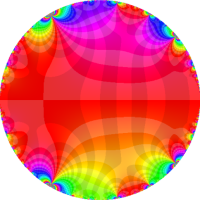
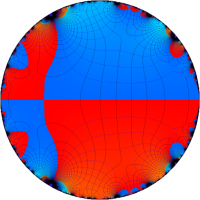
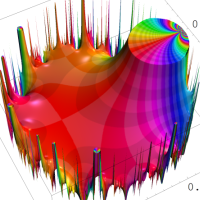
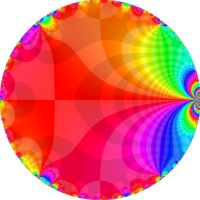
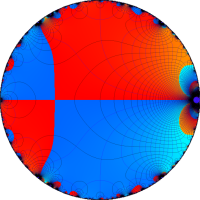
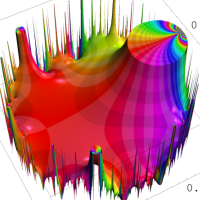
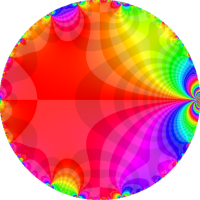
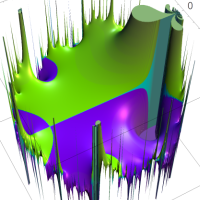
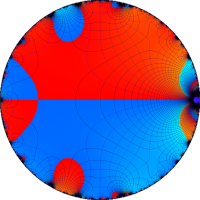
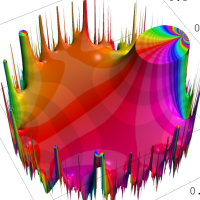
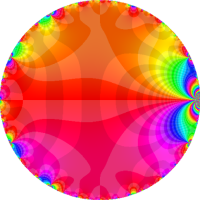
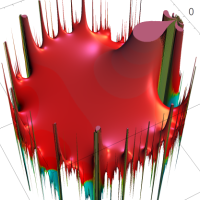
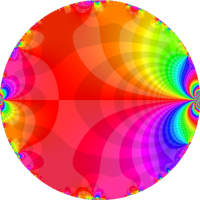
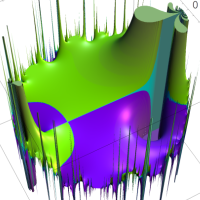
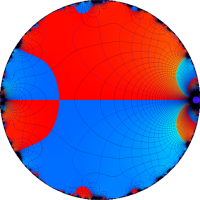
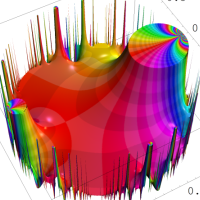
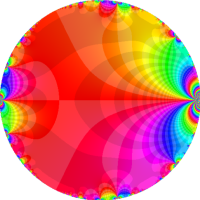
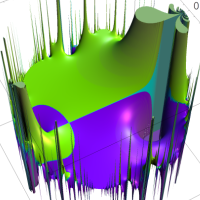
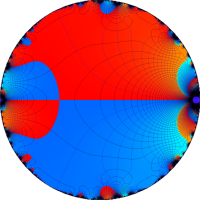
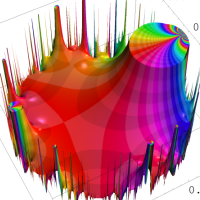
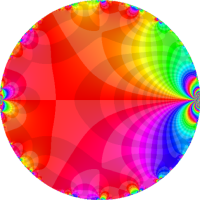
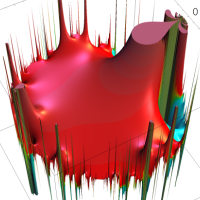
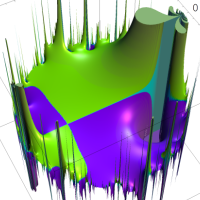
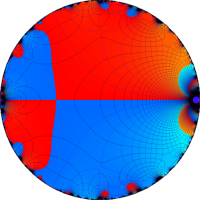
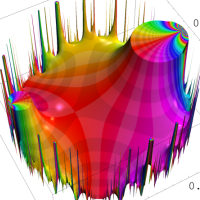
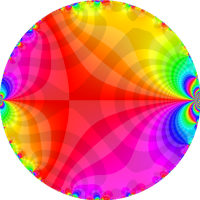
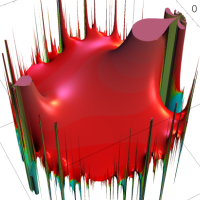
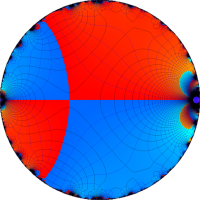
　複素変数の Rogers - Ramanujan 連分数のグラフ。単位円の外部は、正20面体方程式に付随する楕円モジュラー関数を単位円の内部から外部へ反転した関数と一致する (解析接続ではなく計算の一手法として)。

• 
• 
• 
• 
• 

Rogers - Selberg 恒等式

　以降は、Wolfram MathWorld の q-級数の頁 (http://mathworld.wolfram.com/topics/q-Series.html) に記述のある、いくつかの恒等式について考察する。
　Rogers - Selberg 恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。
　(以下同様に、なる記法とする。また、関数記号は独自に定めたものである。)

　複素変数の Rogers - Selberg 恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Rogers - Selberg 恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Rogers - Selberg 恒等式のグラフ。

• 
• 
• 
• 
• 

Jackson - Slater 恒等式

　Jackson - Slater 恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。

　複素変数の Jackson - Slater 恒等式のグラフ。

• 
• 
• 
• 
• 

Göllnitz - Gordon 恒等式

　Göllnitz - Gordon 恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。

　複素変数の Göllnitz - Gordon 恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Göllnitz - Gordon 恒等式のグラフ。

• 
• 
• 
• 
• 

Bailey Mod9恒等式

　Bailey Mod９恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。

　複素変数の Bailey Mod９恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Bailey Mod９恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Bailey Mod９恒等式のグラフ。

• 
• 
• 
• 
• 

Rogers Mod14恒等式

　Rogers Mod14恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。

　複素変数の Rogers Mod14恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Rogers Mod14恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Rogers Mod14恒等式のグラフ。

• 
• 
• 
• 
• 

Dyson Mod27恒等式

　Dyson Mod27恒等式とは、

• 

なる q-級数 (の関係を示す恒等式) である。

　複素変数の Dyson Mod27恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Dyson Mod27恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Dyson Mod27恒等式のグラフ。

• 
• 
• 
• 
• 

　複素変数の Dyson Mod27恒等式のグラフ。

• 
• 
• 
• 
•