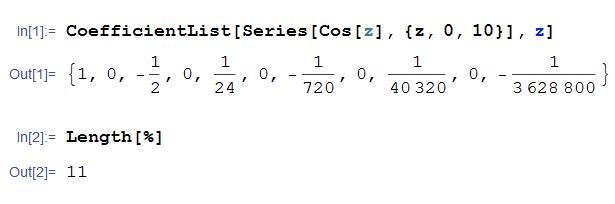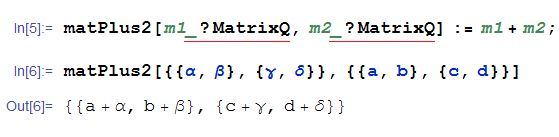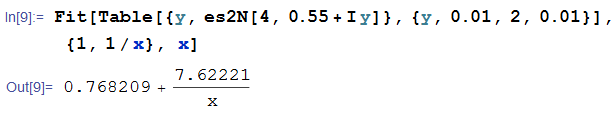特殊関数 グラフィックスライブラリー
Graphics Library of Special functions

Mathematicaの落とし穴

CoefficientListによるリストの長さの判定

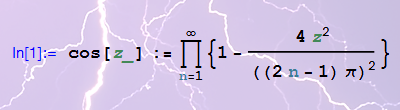
　任意の関数を純関数で指定する引数を持ち、その関数を Maclaurin 展開したときの係数と、その係数リストの長さを内部計算で必要とするようなコードを書いていたとする。ここでは簡単のため、0次～10次の係数 (つまり、11個の要素からなる長さ11のリスト) を仮定する。
　このとき、引数関数が余弦関数ならば、

• 

となり、意図した結果となる。しかし正弦関数ならば、

• 

となってしまう。もし、内部コードでリストの長さの判定条件にこれを使用していたら、エラーが発生する。よって Join[list, {0}] 等を用いて、リストの末尾に要素０を補う必要がある。
　CoefficientList は、元々多項式の係数を求める組み込み関数である。そこで、次のように SeriesCoefficient を使用するのが本来の方法であり、かつオールマイティーな方法であると思われる。

• 

　なお、他の理由、例えば計算速度に関して CoefficientList と SeriesCoefficient のどちらを使うのが望ましいかは、個々の問題や条件によって異なってくると思われるので、実際には動作テストで確認した方がいい。

行列を指定するパターンマッチングでの混乱

　変数がリスト (ベクトル) のときは、パターンマッチングで次のように指定する。

• 

　一方、変数が行列のとき、パターンマッチングで次のように指定すると、うまくいかない。
　(パターンにマッチしないと判断されたため、入力した命令文がそのまま返されるだけとなる。)

• 

　行列のときは、次のように指定すれば意図した動作をする。
　( Mathematica の仕様によるものであり、全く理由はない。)

• 

　これは特に、行列変数とベクトル変数が混在するようなコード内で混同しやすい。

ループ型？ or 関数型？

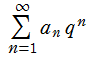　の形の級数を While ループで記述しようとして、次の２通りのコードを書いた。
　（級数展開式の初項が１となるように定数倍した、重みの正規化 Eisenstein 級数の例。）

• 

　後者は意図した結果になる。しかし、前者は級数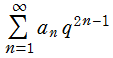になってしまう。

　前者のコードを用いて Klein の楕円モジュラー関数を求めようとしたが、誤った結果になっている。

• 

　後者のコードを用いれば、正しいのグラフになる。

• 

　勿論、局所変数は必須ではなく、もっと簡単な次のコードでも正しい結果になる。

• 

　しかしこのコードは、前の例よりも計算が遅いのである！。

• 

　高速化の定石は、ループ型ではなく、関数型プログラミングを用いることである。しかし、後者にも思わぬ落とし穴がある。以下、その一例を示す。
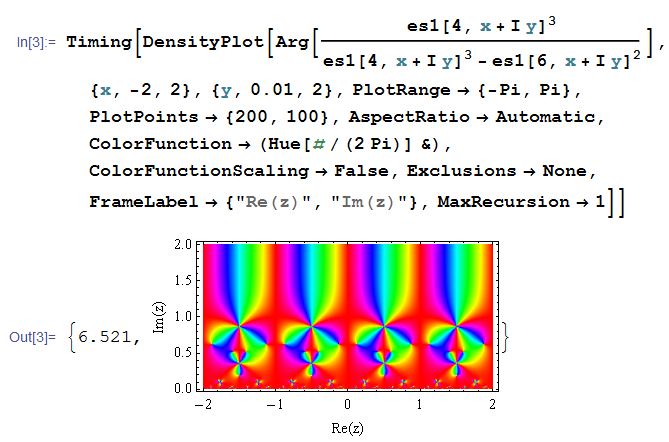
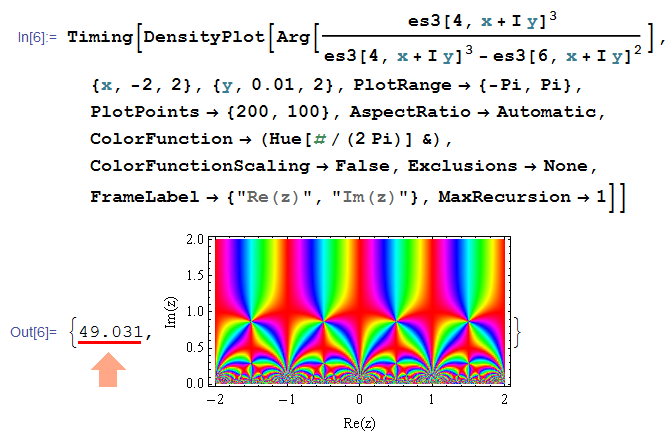
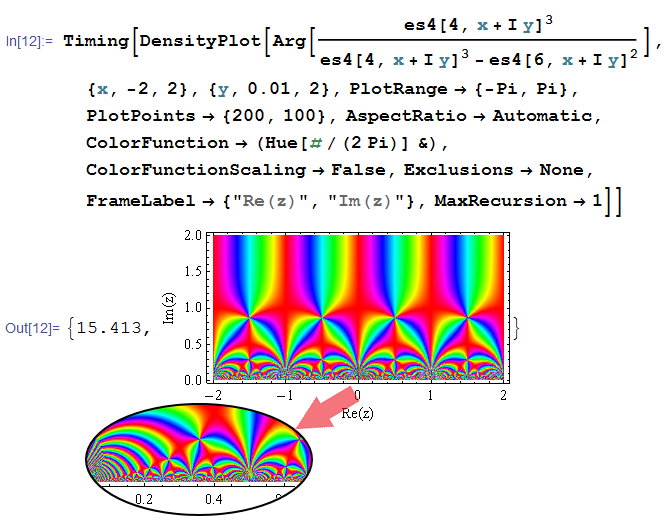
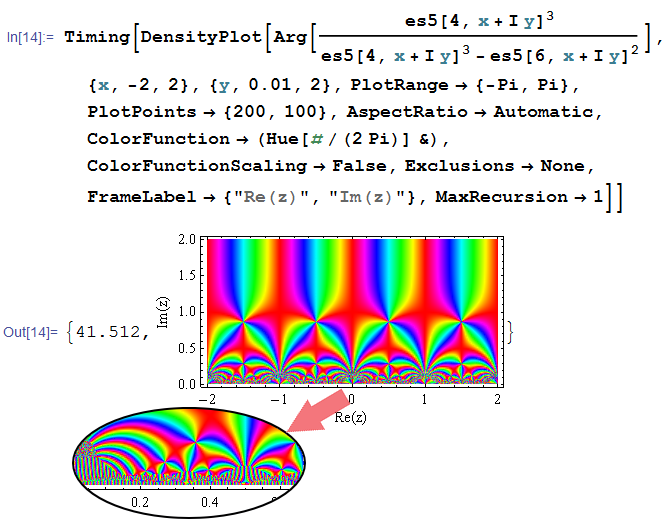
　前にループ型でプログラミングしたコードが、虚部の大きさに応じて反復回数をどのように決めているかを確認する。

• 

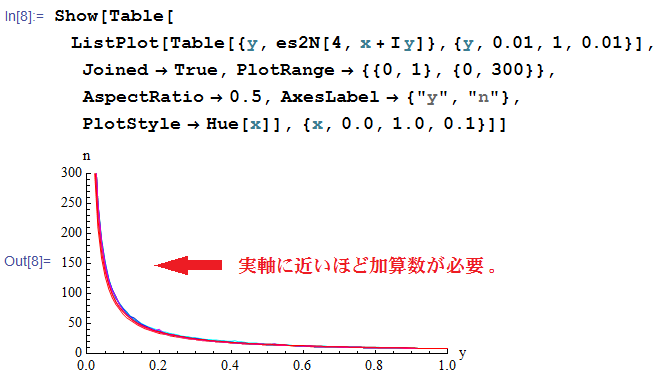
　実部が異なるいくつかの虚軸方向で描画した、反復回数のグラフ。概ね一次分数関数に近いように見える。

• 

　そこで、この曲線に概ね適合する具体的な一次分数関数を求める。

• 

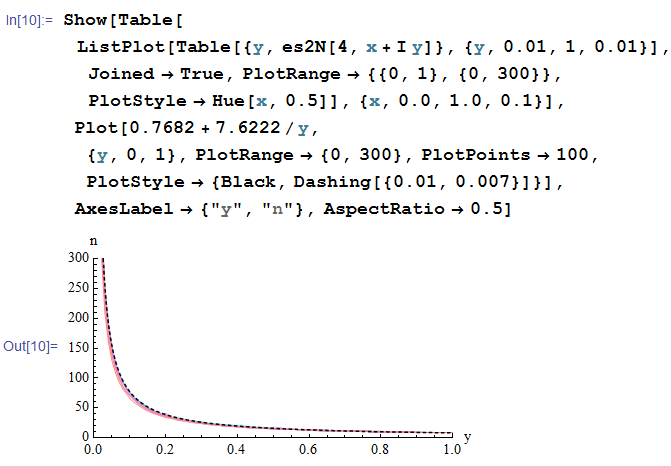
　先の反復回数のグラフと重ねて描画してみると、よくフィットしていることが分かる。

• 

　この結果を用いて、関数型プログラミングを作成する。

• 

　これまでで最も高速である。

• 

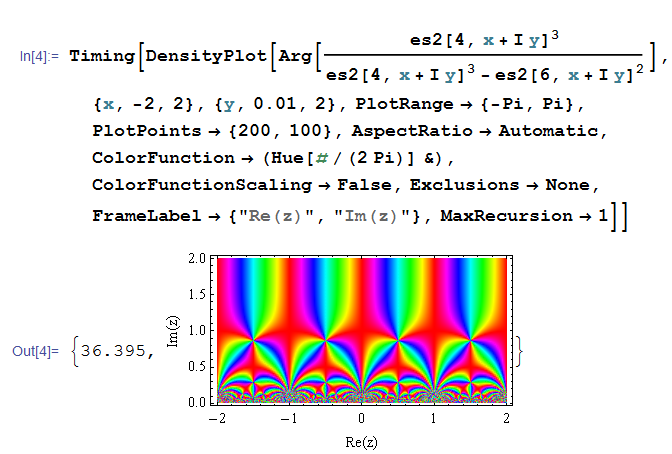
　もし、上記のような加算回数の見積を行わず、単に固定回数で関数型プログラミングを作成すると、どのような結果になるか確認する。

• 

　実軸の近傍では加算回数不足のため不正確になっている。逆に虚部が大きい領域では回数が冗長なため余分に時間がかかり、全体として遅くなっている。関数型プログラミングは記述しやすく高速だが、被プログラミング関数の特性をよく踏まえないと、この事例のように本来の利点が発揮できない場合もある (つまり万能ではない) 。

• 

等高線は悩ましい

【その1：Throw::nocatch エラー】
　MeshFunctions は、等高線を引く位置を決める関数を指定するオプションである。その位置関数は ｢純関数｣ で表現することになっており、純関数は Function または Slot () の2通りの方法で記述できる。
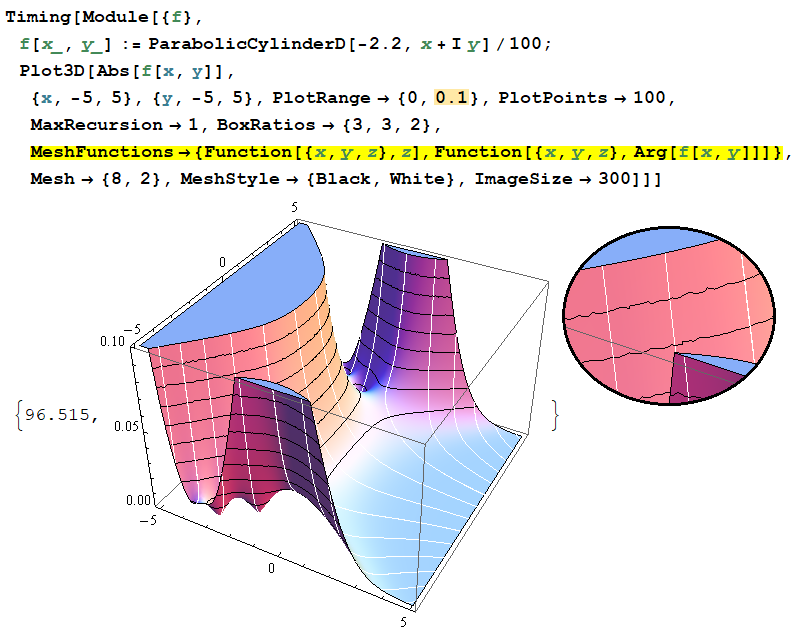
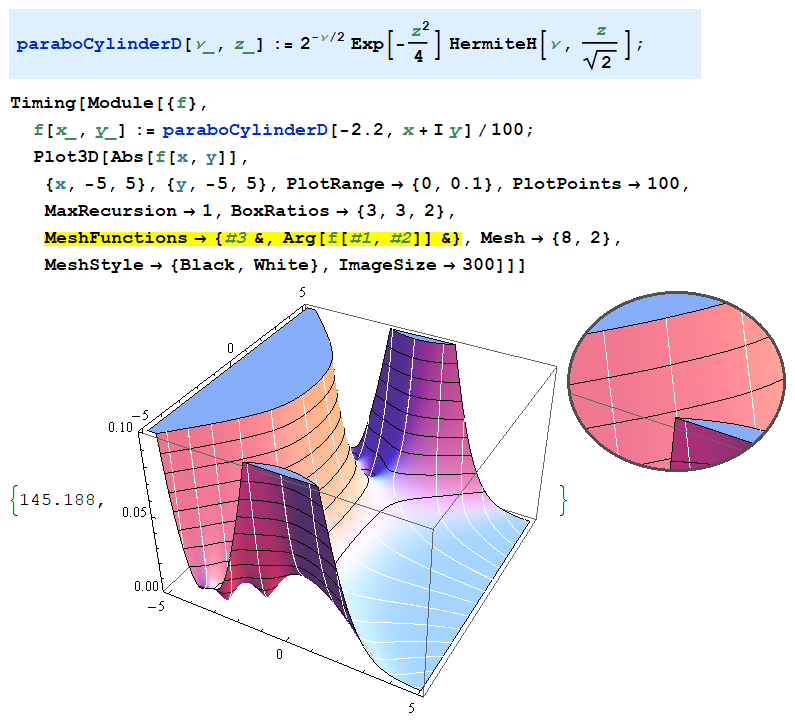
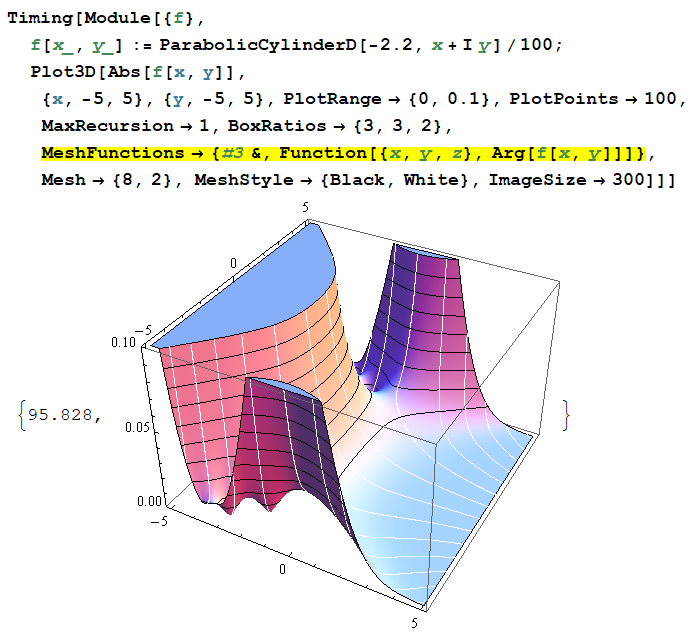
　次のコードは、Function で記述した場合であるが、PlotRange の上限値が０に近いグラフでは、絶対値の等高線が乱れる。(以降、絶対値の等高線は黒、偏角の等高線は白で描画する。)

• 

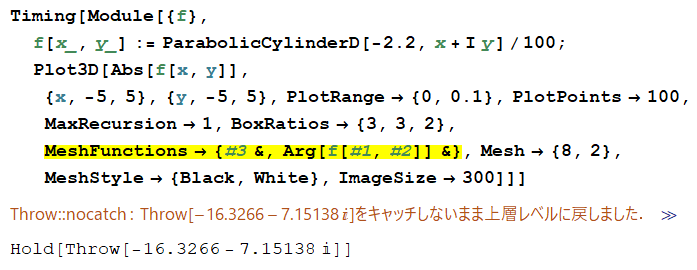
　純関数を Slot で記述した場合は、エラー Throw::nocatch が発生して計算が強制終了する。

• 

　ParabolicCylinderD は HermiteH で記述できる。そうすれば Throw::nocatch は発生しないので、このエラーの原因は ParabolicCylinderD にあることが分かる。(しかし、その理由は不明。)
　因みに、純関数を Slot で記述した場合、絶対値の等高線は乱れない。

• 

　後述するとおり、ParabolicCylinderD と同様のエラーが発生する Mathematica 組込の複素関数は、いくつか存在する。
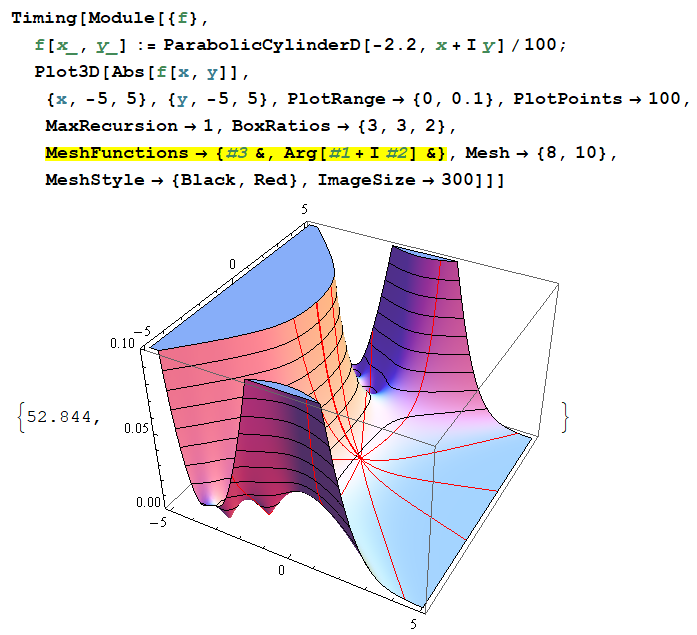
　どの組込関数であってもエラーが発生せず、しかも常に絶対値の等高線が乱れない方法として、次の (やや奇妙な) 折衷策が有効となる。この方法は、MathematicalFunctionPlot.m にも採用している。

• 

　偏角の等高線にはなっていないが、純関数 Slot でおよびを用いること自体に問題はないことが、次のコードから分かる。

• 

　恐らく、およびを ParabolicCylinderD 内で使用することに問題がある。(つまり、局所記号が原因ではない。)

• 

　因みに ColorFunction も純関数で指定するオプションである。これも同様に、純関数を Function で記述した場合はエラーにならないが、Slot の場合はエラーが発生する。(MathematicalFunctionPlot.m は Function を使用している。)

• 

• 

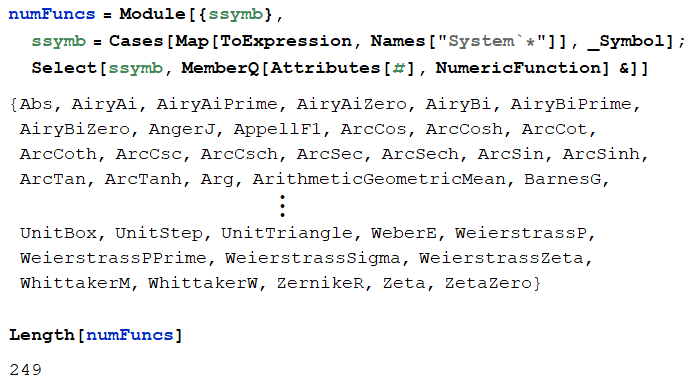
　そこで、Mathematica 組込の複素関数のほとんど全て (ただし、Ver.8 時点) について、ParabolicCylinderD と同様の問題が発生するか調査した。
　次は、属性が ｢NumericFunction｣ である組込関数名をシステムから抽出する方法である。

• 

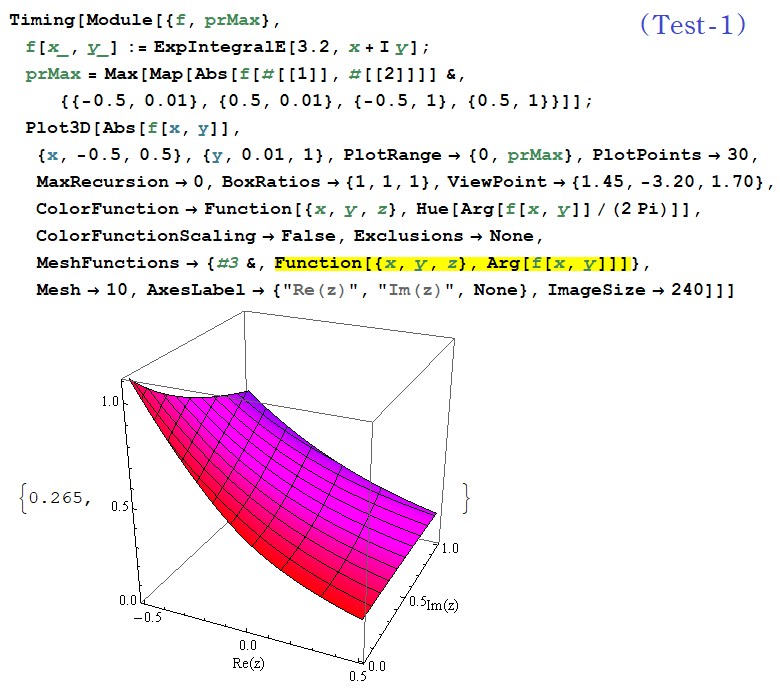
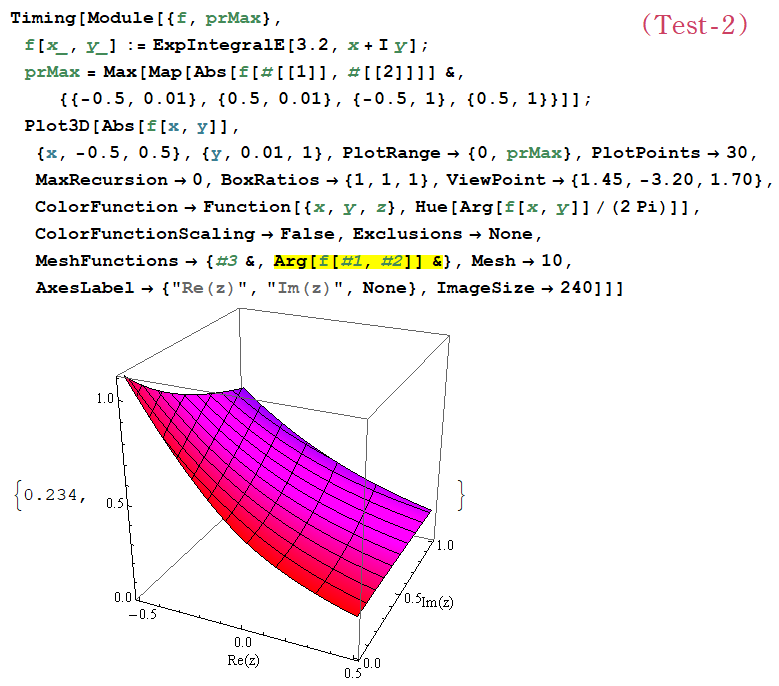
　上記のうち、複素変数グラフを描画する可能性のある組込関数を手動で選び★、その各々について次の2種類の描画テストを実行し、｢Test-1｣ は問題なく描画できる事を、｢Test-2｣ は問題が発生するかどうかを確認する。
　（の右辺、およびは、その都度 書き換えて実行する。★で取り除いた関数の例として、変数が自然数のみで定義される AiryAiZero、複素関数を考える事ができても Mathematica では引数が実数に限る InverseErf, BSplineBasis 等がある。）

• 

• 

（調査結果）
　2種類の描画テストのうち、Test-1 は全ての組込関数で描画可能、Test-2 は①②以外の全ての組込関数ならば描画可能であることが判明した。
　（①②については、描画範囲, 描画精度, 関数や引数の定数倍, 等高線の本数または間隔等を、様々 (整数の他にも、無理数を使用する等) に取り替えてテストしましたが、問題の発生状況に違いは無いようです。このことから、ある特定の値が Throw::nocatch を発生させている可能性も低いです。なお、Ver.9以降での動作、他のPC環境での動作がどうなるか大変気になりますが、これについては確認していません。）


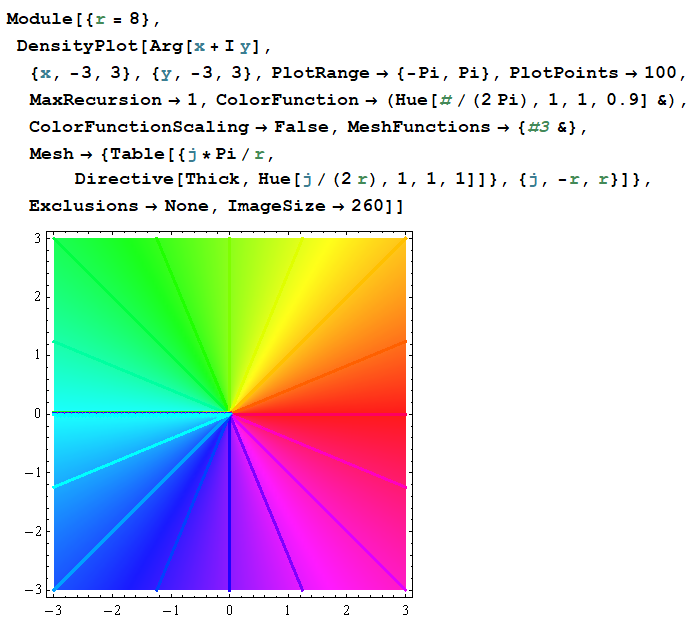
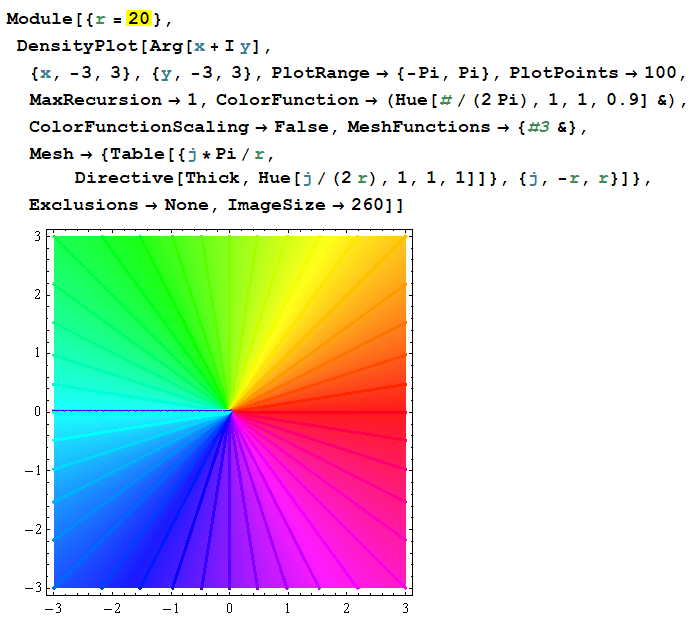
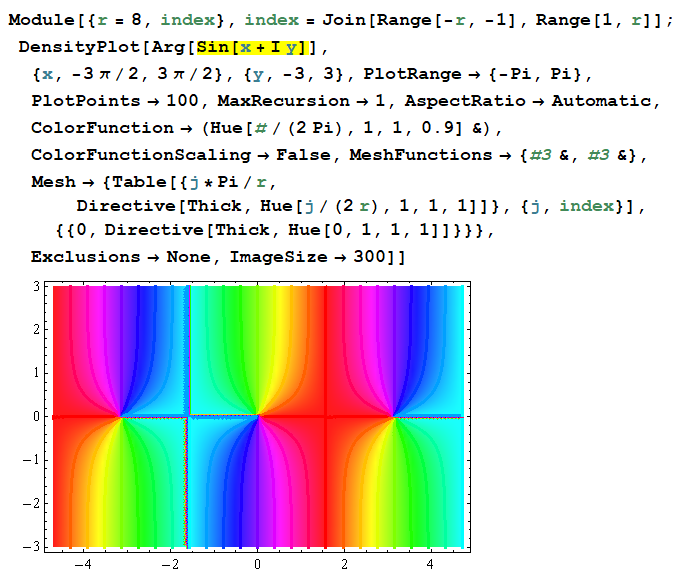
【その2：偏角等高線の彩色】
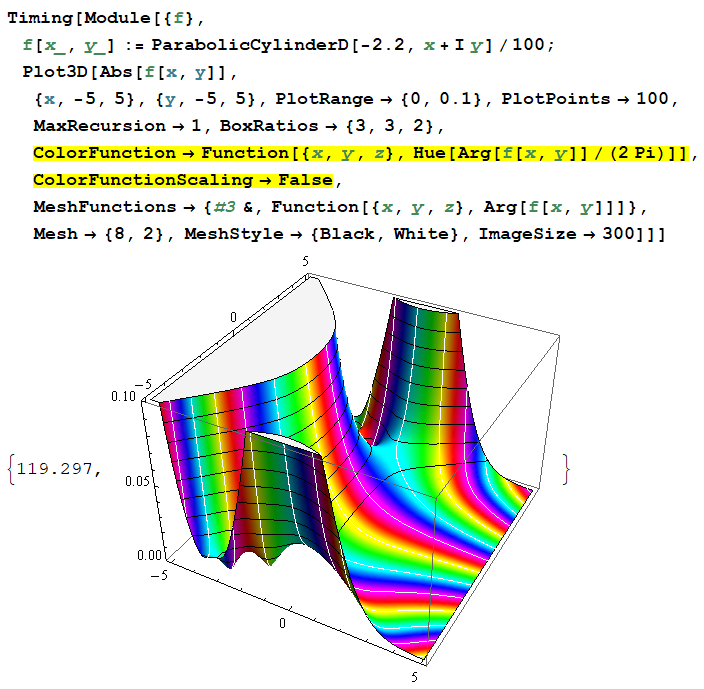
　偏角の等高線を色相環に基づいて彩色する。しかし、明らかに ColorFunction の色相と一致していない。

• 

　等高線の本数は、この問題と関係ない。

• 

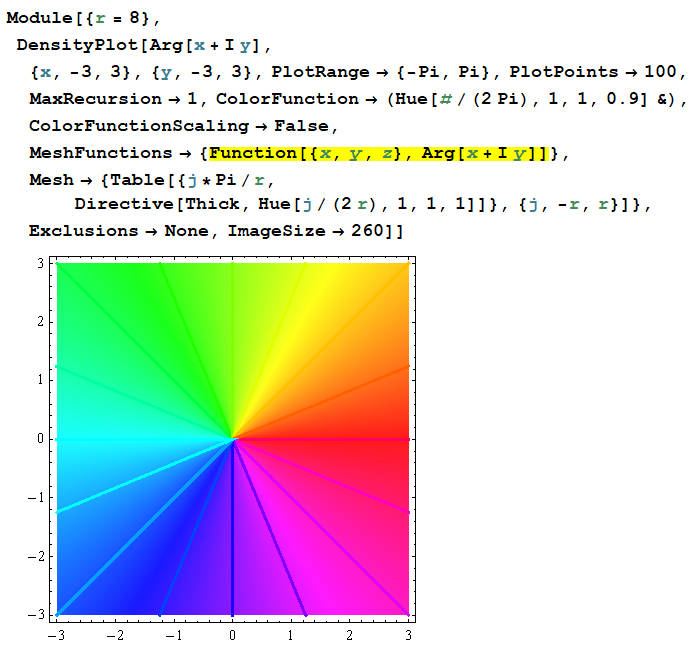
　MeshFunctions の純関数を Slot () ではなく Function で記述しても、色相の不一致が起きる。

• 

　Mesh の指定から、となるインデックスのみを取り除くと、なぜか色相が一致する。(理由は不明。)

• 

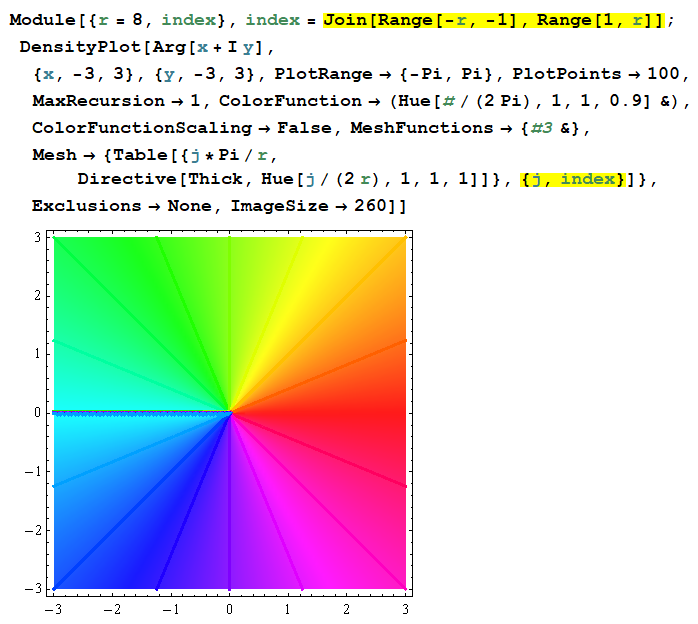
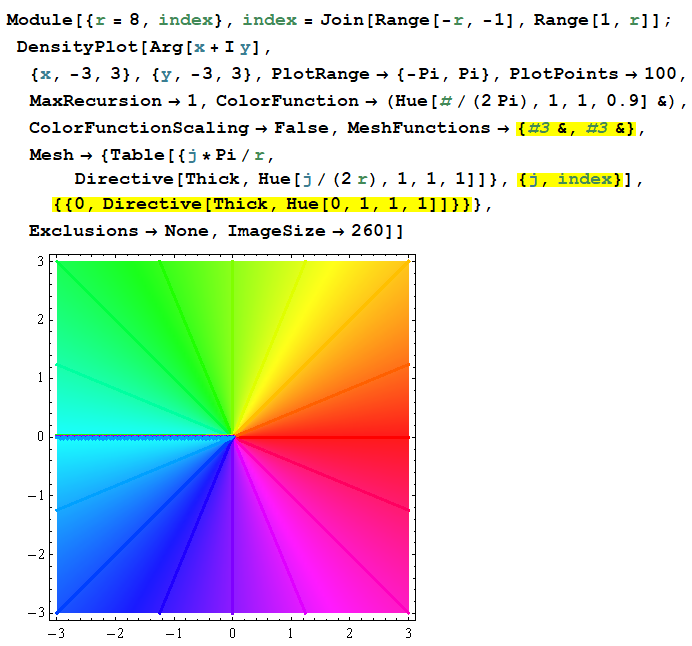
　よって、次のように記述すれば良い。(ただし、偏角がの等高線は太くなる事が、別の問題として残る。)

• 

　正弦関数の場合。

• 

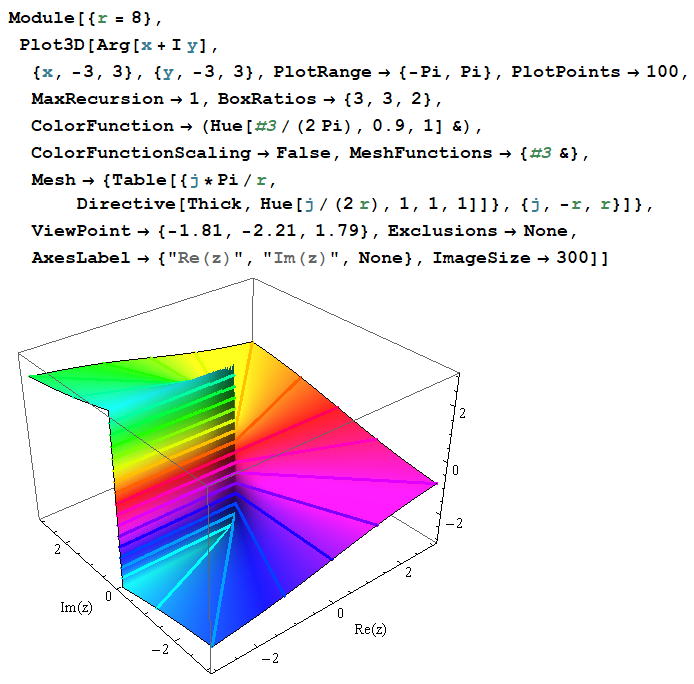
　色相の不一致は、Plot3D でも起きる。

• 

　DensityPlot での方法を応用すれば、同様に色相は一致する。(しかし、依然として理由は分からない…。一方、偏角がの等高線のみ太くなる理由ならばこの図から分かる。すなわち、複数の等高線が重なっていることによる。)

• 

• 

•