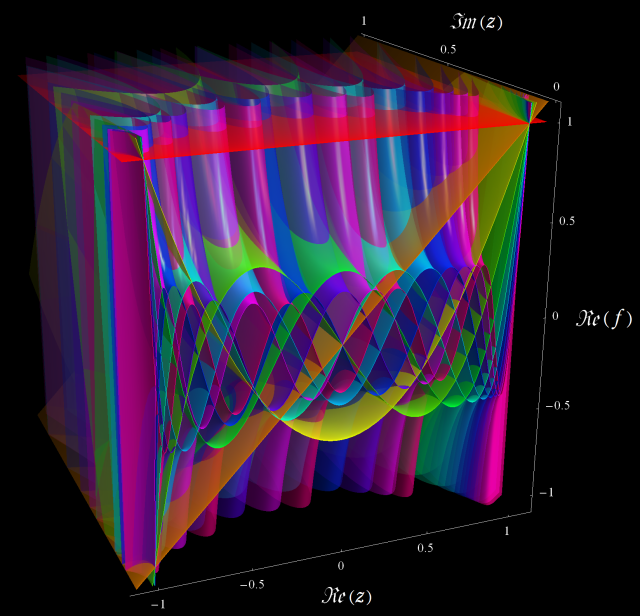
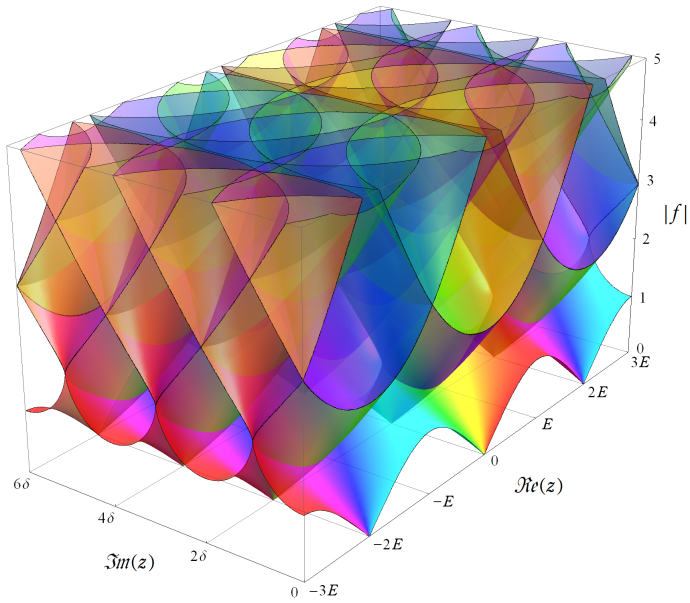
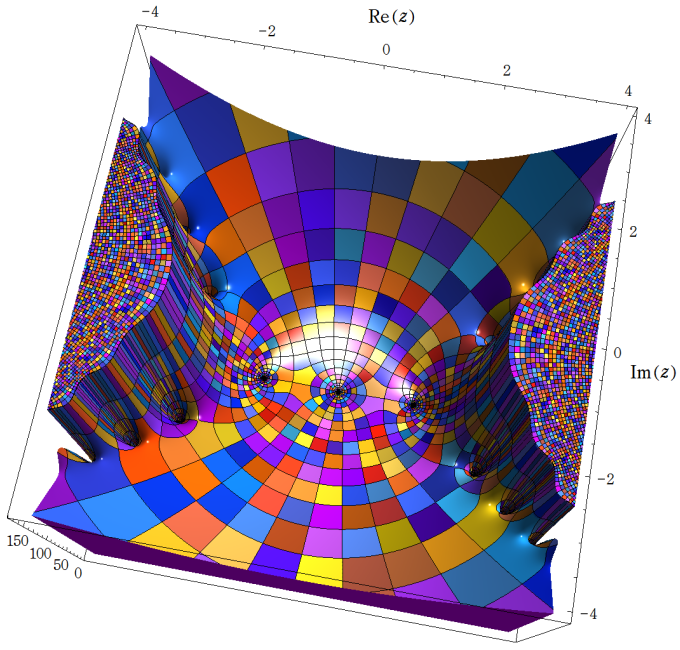
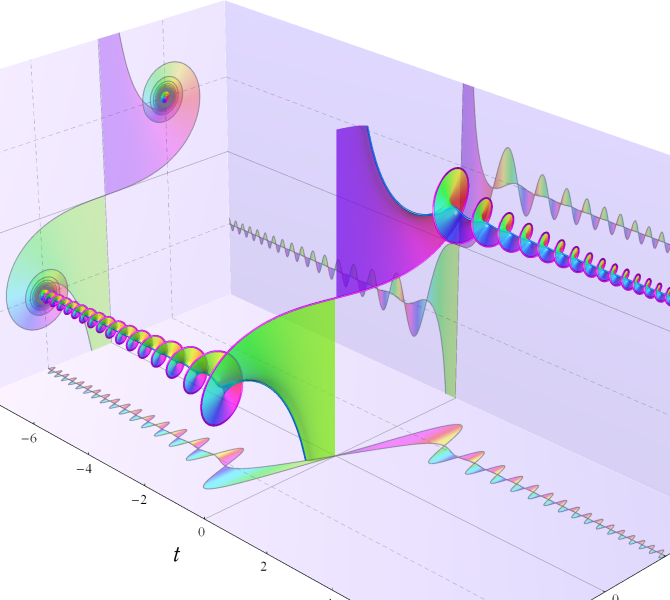
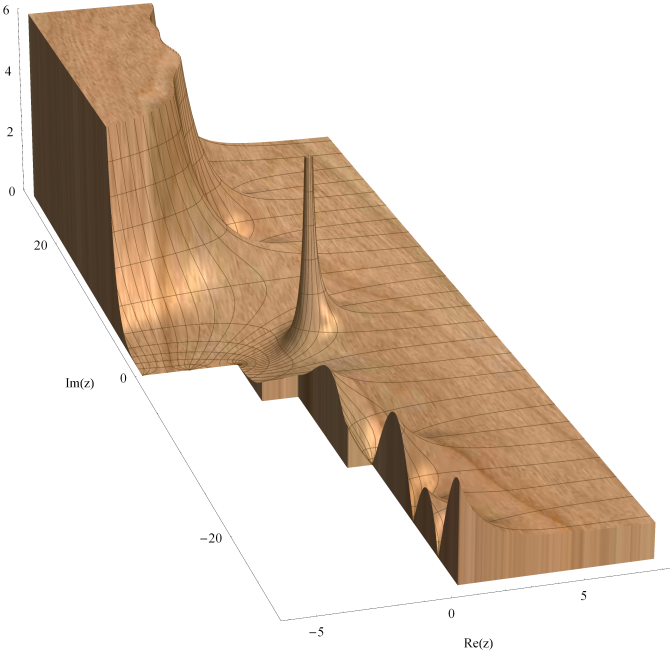
特殊関数 グラフィックスライブラリー
Graphics Library of Special functions
http://math-functions-1.watson.jp
Ｈｏｍｅ Menu
壮麗かつ深遠な特殊関数の世界
複素変数の場合を中心とする約9000個のグラフ・アニメーションによる視覚化、数学への興味が湧く不思議な公式・話題、Mathematicaによるプログラミング例、etc.…
New & Modified（古い画像が表示されるとき → 対処法）
① s＝4 および 3 における Fibonacci ゼータ関数の特殊値 (2024年6月22日)
New & Modified（古い画像が表示されるとき → 対処法）
① s＝4 および 3 における Fibonacci ゼータ関数の特殊値 (2024年6月22日)
Gallery
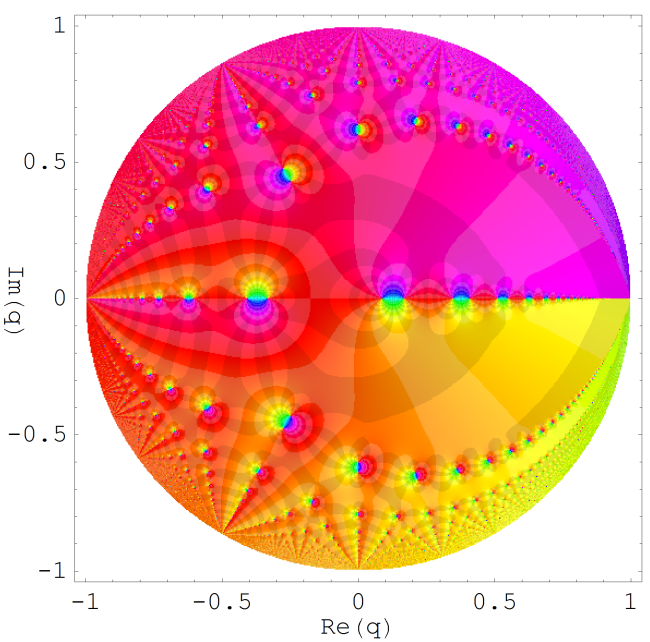
Riemann 球面上の Galois 的有理関数
この関数は、楕円型非 Euclid 平面 (Riemann 球面) 上の保型関数である。絶対値は逆双曲線正弦的、彩色は初代 iMac 風。
複素変数の Legendre 多項式 (実部) の重ね合わせ
実軸上の断面にある Legendre 多項式を虚数方向に延長する。
第2種楕円積分 (Legendre - Jacobi の標準形) の逆関数
楕円関数と同様に二重周期関数であるが、一価ではなく無限多価関数となる。(→ 第2種楕円積分, 描画方法)
第2種 Hermite 関数
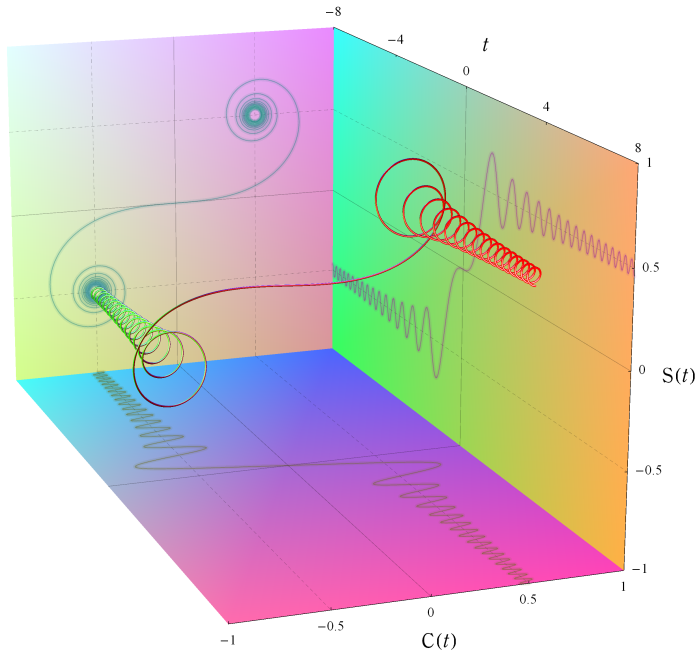
等高線で分割された領域を乱数に基づいて彩色する。(→ Hermite 関数)
クロソイド曲線とその縮閉線
空間曲線化と三方向への射影。色相は曲率半径の傾斜角度に基づく。(→ Wikipedia : 縮閉線)
Jacobi の楕円振幅関数
石膏模型風にした Jacobi の楕円振幅関数のグラフ。
実解析的 Eisenstein 級数
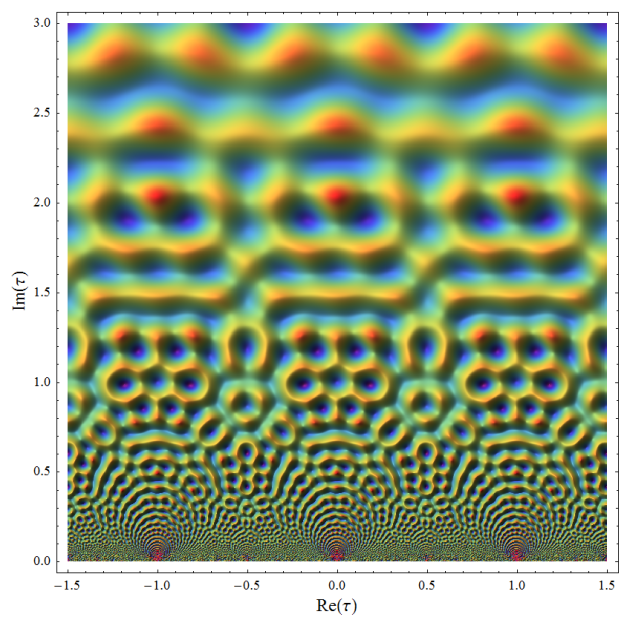
ReliefPlot による実解析的 Eisenstein 級数のグラフ。
クロソイド曲線弧で分割配色された Weierstrass の楕円関数
クロソイド曲線弧の歪三角形によるタイル貼り模様で Weierstrass の楕円関数を配色する。垂直軸は逆双曲線正弦的。
Julia 集合の外部に等角写像された保型関数
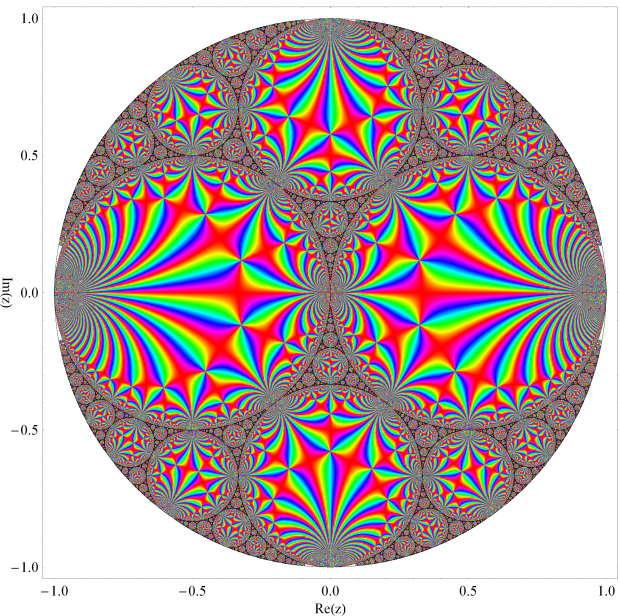
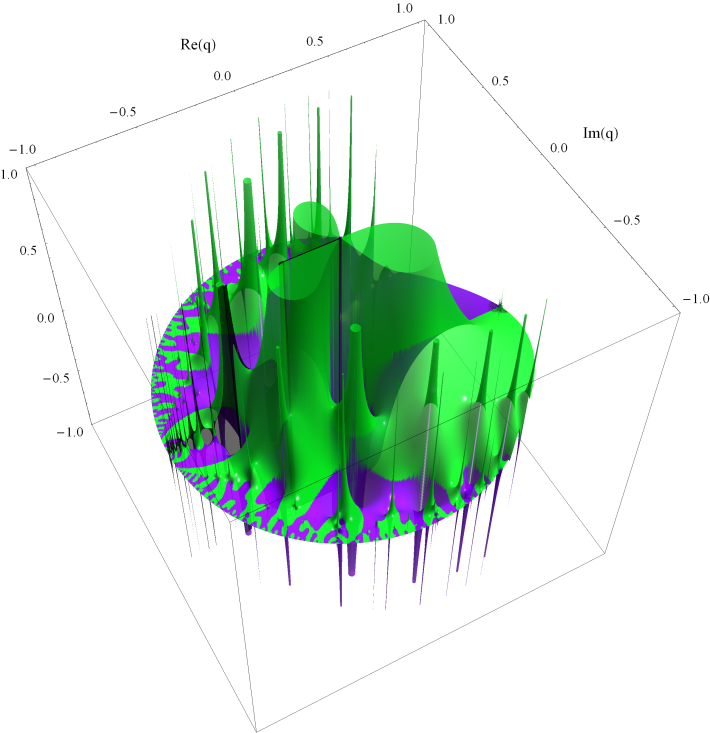
Böttcher 関数によって Schwarz の保型関数を Julia 集合の外部に移す。垂直軸は逆双曲線正弦的。
Klein の楕円モジュラー関数による「Apollonian gasket」
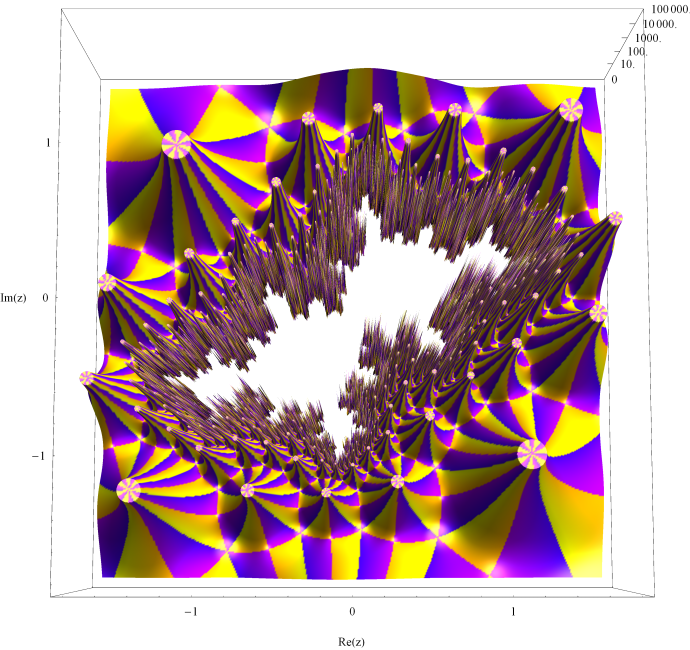
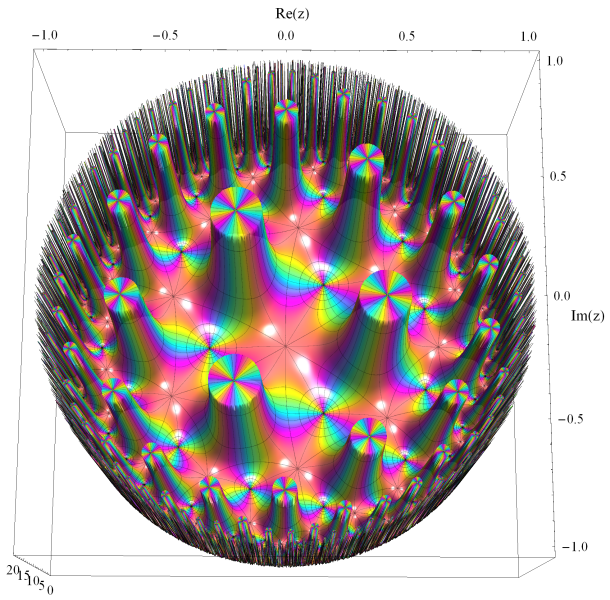
存在領域が円である Klein の楕円モジュラー関数を用いて、単位円の内部を充填する。
第5種 Painlevé 超越関数
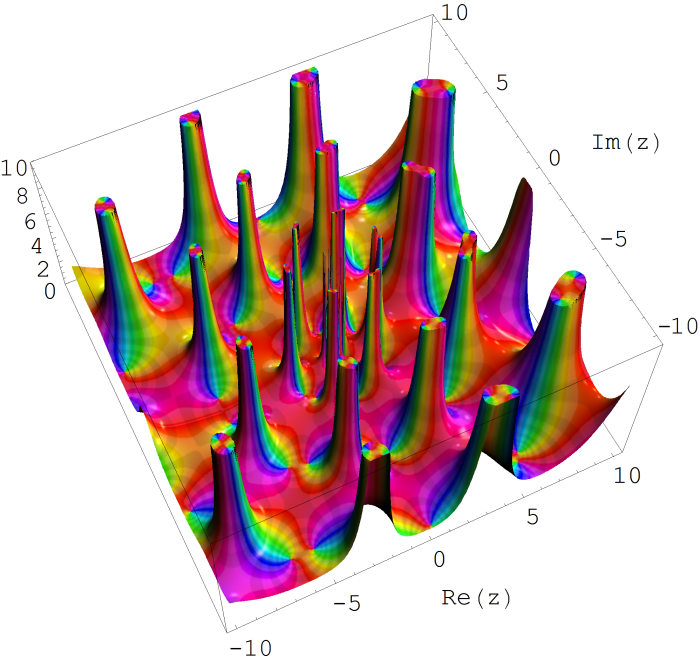
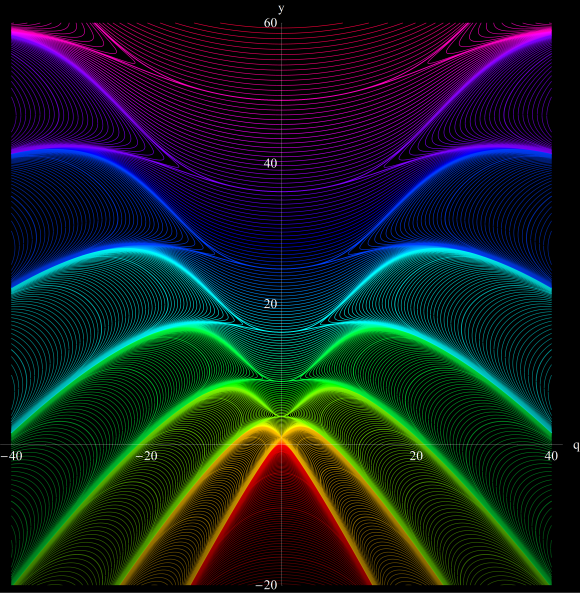
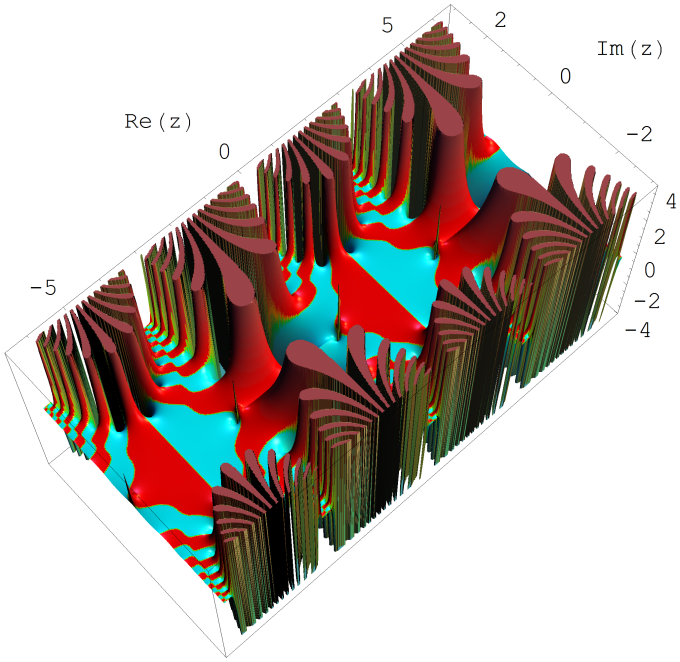
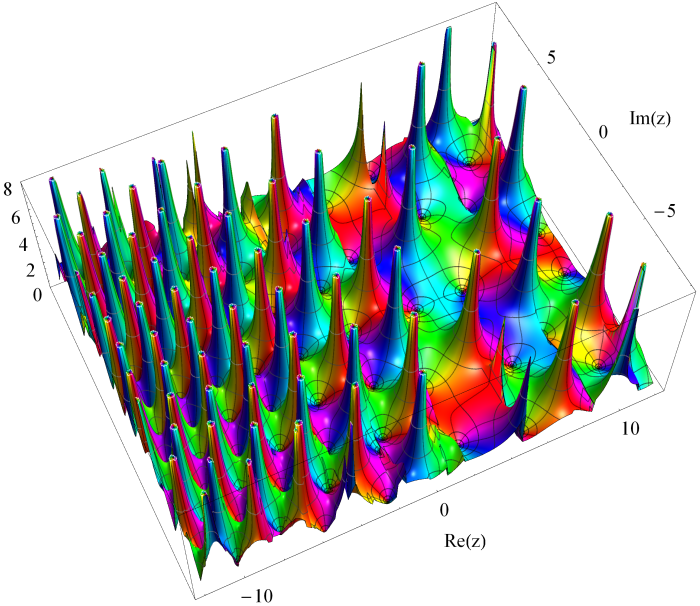
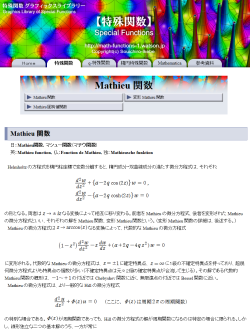
第5種 Painlevé 超越関数は原点に動かない分岐点を持ち、通常は負の実軸上に分枝切断線を置く。
Mathieu 固有値関数
Mathieu 関数の様々な次数に対する、固有値のとりうる値。 安定域と不安定域を重ねて描画。
Fresnel 関数およびクロソイド曲線
Fresnel 関数とクロソイド曲線の射影元となる、エレガントな空間曲線。
Jacobi の第2種楕円関数（Jacobi の楕円イプシロン関数）
母数が複素数となる場合。この関数は楕円関数を積分したものに相当する。
Schwarz の保型関数
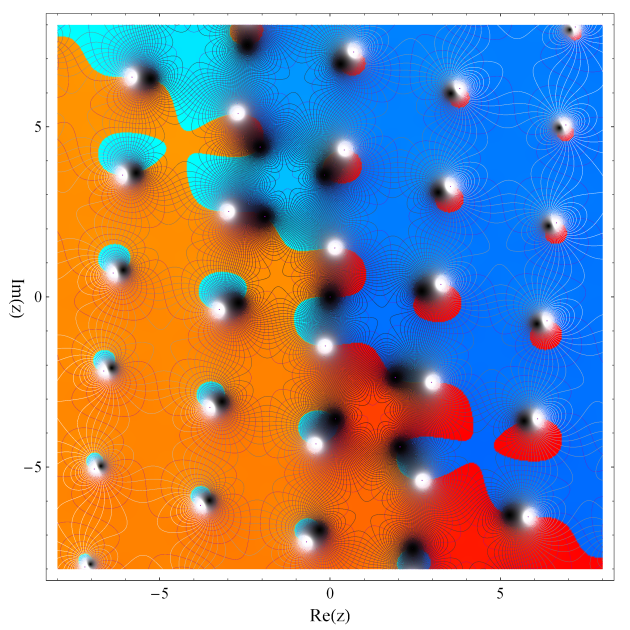
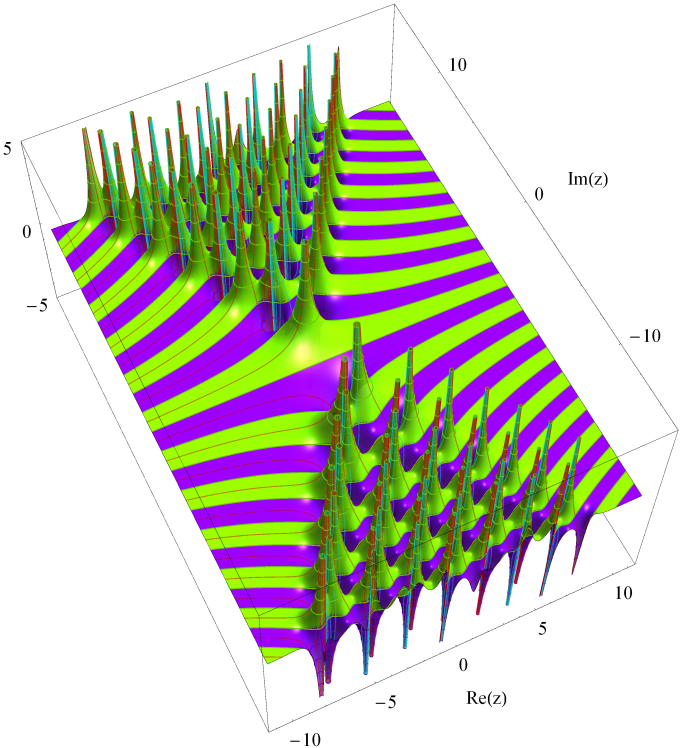
楕円モジュラー関数ではない保型関数の一例。Fuchs 関数の一種。
第2種 q-Bessel 関数（変数：q）
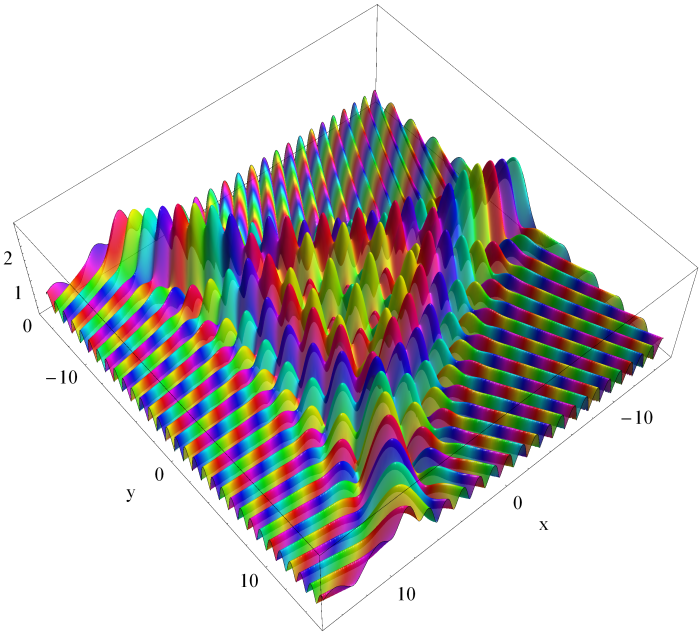
単位円の近傍で複雑な様相を呈する。(→ q-Bessel関数)
第2種扁長回転楕円体波動余弦関数
第2種の回転楕円体波動関数(スフェロイド関数)に余弦関数を代入した関数。
q-対数関数（変数：q）
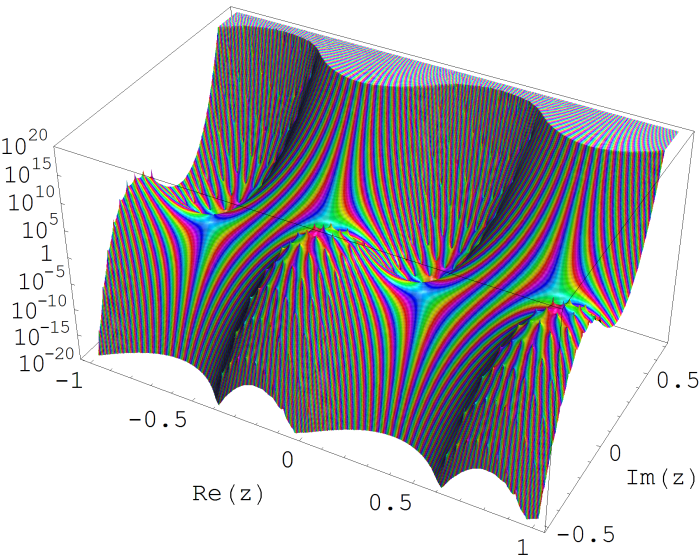
単位円周への特異点の美しい集積。(→ q-対数関数)
楕円ガンマ関数
垂直軸は常用対数的スケール。関数値の急激な増大と無数の特異点。(→ 楕円ガンマ関数)
楕円形膜の振動
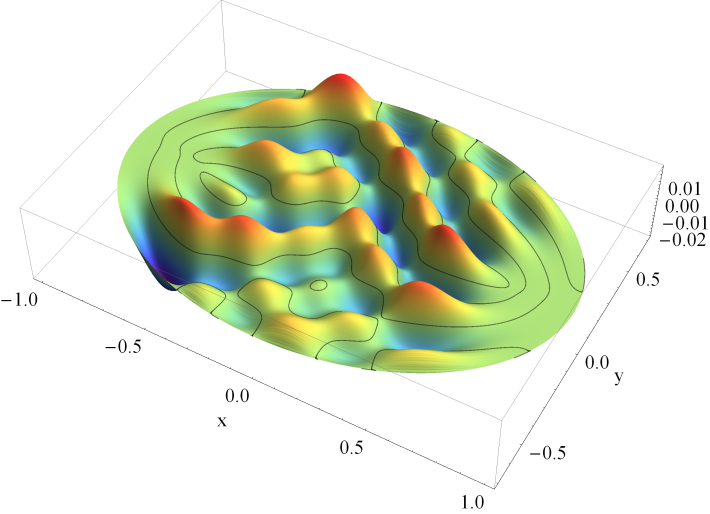
固有振動を重ね合わせた現実に近い振動。Mathieu 関数を使用する。(→ 楕円形膜の振動)
非強制振動型 Duffing 関数
強制振動項を持たない Duffing の微分方程式の解を、複素関数として描画する。(→ 非強制振動型 Duffing 関数)
楕円的臍点正準積分関数（Elliptic umbilic canonical integral function）
楕円的臍と呼ばれるカタストロフィー現象と関係する積分関数。(→ この関数の詳細)
第1種 Muğan-Jrad 超越関数
対数微分すると、第2種 Painlevé 超越関数になる場合。(→ この関数の詳細)
Mathematica のテクスチャー効果を用いた例
木製のオブジェ (Riemann のゼータ関数)。E. Jahnke，F. Emde 著「Tables of Functions with formulae and curves」にある図と同等のグラフ。
大理石のオブジェ (Jacobi の楕円関数)。
お詫び・留意事項
当サイトへのリンクを張る場合等の注意事項（重要）
注意事項 (Notes)！の頁にある規約を必ずご確認の上、遵守願います。
グラフを描画した時のコードは頁上には表示しておりません
具体的な描画範囲などを知りたい場合は、お手数ですが Mathematica関連 の頁にある Mathematicaノートブックファイルをダウンロードしてご確認ください。
Mathematicaがインストールされていない端末では、ダウンロード後にテキストファイル形式へ変換すれば、コードを確認できます。また、無料の「Wolfram CDF Player」をダウンロードする方法もあります。
http://www.wolfram.com/products/player/
（注意：「Wolfram Player Pro」は有料。）
なお、いずれの場合も、計算の実行はできません。
コードを実行して生じた故障・不具合は、当サイト管理者は一切責任を負いません
問題が無い場合でも、当サイトに掲示している複素変数のグラフと同等精度の画像を得ようとすれば、１グラフあたり大抵２～３時間はかかります(数日を要するものも存在します)。また計算中は、CPU使用量やメモリーもある程度占有し、端末にかなりの負荷がかかると思われます。特に楕円体関数系の固有値は、瞬間的にCPU使用量が跳ね上がることを確認しています。
いずれのコードも、少なくとも一度は計算に使用した経歴のあるものですが、あくまで素人が作成したものであり、予期できない不具合が生じる可能性があります。恐れ入りますが、ご自身で計算を試される場合は自己責任でお願いします。
特に、描画精度 (PlotPoints, MaxRecursion等) を更にアップさせた訂正コードで実行する場合は注意が必要です。(元コードでも既に精度が過剰気味。逆に初回計算では精度を下げ、所要時間の大まかな見積と、CPU･メモリーメーターの監視をお勧めします。)
コード内の特殊関数は、変数のすべての領域で計算できるとは限りません
「Mathematica関連」頁にある 特殊関数のコードは、元々グラフを描画する目的に特化したものであるため、関数の種類によっては、当サイトに掲示したグラフの描画範囲を超える変数を指定した場合、不正確な値または計算不能となることがあります。
（例1）Mathieu関数(GeneralizedMathieuを除く), 回転楕円体波動関数等 → 次数が整数次の場合のみ計算可能。
（例2）Painlevé 超越関数等 → 原点から遠い領域(絶対値が約20以上など)では不正確。
使用文体の混在等
特に、学術的色彩の強い箇所では「～である」調を採用したため、「～です」調と混在しています。
また、正しい仮名送り法が複数ある場合で、一般的でないほうを採用しているものがあります。
（例）表される→表わされる
公式の定義について
特殊関数は通常、同じ名称のものであっても異なる定義が存在します。当サイトに記述した公式や数式のいくつかは、一般的でない表記法を採用しています。例えば、楕円積分・楕円関数系では母数(第2変数)の記述方法が標準的な公式集のそれとは異なる Mathematicaでの用法に従っています。
記述している公式等を用いる場合は、必ずご自身の目的に合致した定義であるかを、すみませんが公式集等でご確認願います。
工事中の箇所と更新について
「工事中」と表示された箇所は、記事の新設を予定している箇所です (削除する場合もあります)。記事の更新や訂正が長期間されない場合もあることをご了承願います。一方、工事中でない箇所も、予告なく内容等を大幅に変更することがあります。
通信手段について
誠に申し訳ありませんが、電子メールボックスの頁は設けておりません。また、Facebook, Twitter 等のアカウントも所持しておりません。
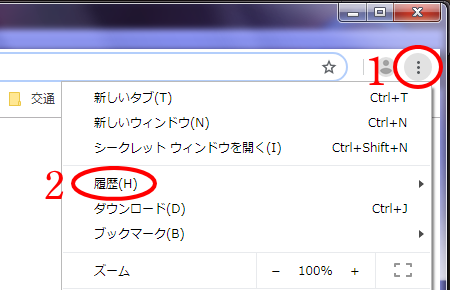
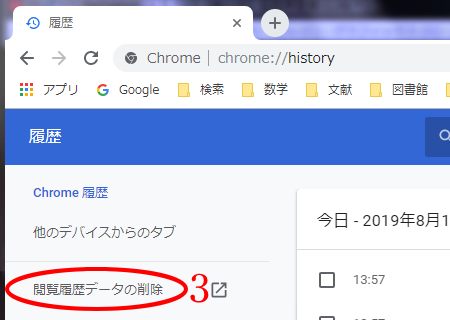
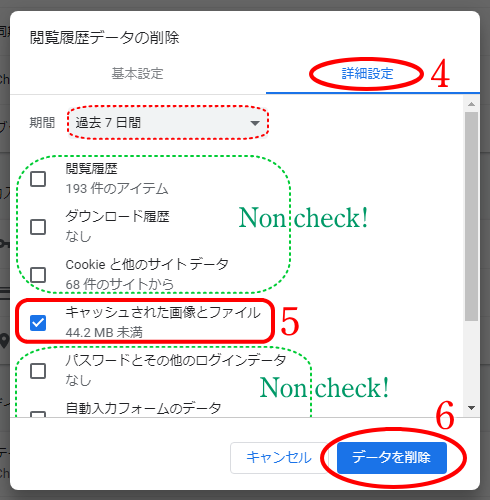
古い画像が表示されてしまうときの対処法
内容が大きく更新された頁を開いたとき、数週間は古い画像が表示され、位置もずれて表示されることがあります (次の画面キャプチャを参照)。
そこで、以下では Chrome を例にキャッシュの削除方法を説明します。(削除後は、サイト等の読込速度が初回のみ遅くなります。)
【削除方法】
① Chrome の右上にあるボタン ｢Google Chrome の設定｣ を押すと、プルダウンメニューが開きます。
② プルダウンメニュー中の、｢履歴(H)｣ を選びます。
（Select "History" in the Pull-down menu.）
③ 左側にあるサイドメニュー中の、｢閲覧履歴データの削除｣ を選びます。
④ ｢詳細設定｣ を選びます。(デフォールトで選択されているかも。)
⑤ ｢キャッシュされた画像とファイル｣ のみチェックを入れ、他の項目はすべてチェックを外します。
（Check only "Cached images and files".）
このとき状況に応じて、｢期間｣ を任意に設定してもよい。
⑥ 右下にある青いボタン ｢データを削除｣ を押す。
⑦ 以上で完了です。当サイトに再アクセスして下さい。
更新履歴 (軽微な更新は除く)
200X年XX月XX日～ … グラフ等の作成開始（ただし公開を予定しない個人用資料として）2011年11月11日～2013年09月17日 … 前身サイト「Painlevé 超越関数の視覚化」
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
2013年09月17日 … サイト「特殊関数 グラフィックスライブラリー」の初公開
2013年09月25日 … 「Riemann のＰ関数」の新規追加
2013年11月14日 … 「Appell-Lerch 級数」の新規追加
2013年11月14日 … 「超楕円積分の逆関数(現：超レムニスケート関数)」の一部変更
2014年01月09日 … 主要な関数名について各国語表記を記述（兼 keyword 用）
2014年01月30日 … 「Abel 関数」の一部変更
2014年03月10日 … 「Meijer のＧ関数」の新規追加
2014年03月28日 … 「Blasius 関数」の新規追加
2014年06月27日 … 「Böttcher 関数」の新規追加
2014年06月27日 … 「Mathematica の(微妙な)Tips」の一部変更
2014年08月16日 … 「非自明零点に関する Dirichlet 級数」の新規追加
2014年08月16日 … 「Sitaramachandrarao 関数」の修正
2014年08月20日 … 「Glaisher - Ramanujan 関数」を「Eisenstein 級数」に統合
2014年09月07日 … 「Lamé 関数」のグラフを変更（Ver.8 化）
2014年09月16日 … 「Kelvin's ship - wave pattern」の新規追加
2014年09月19日 … 「Lamé 多項式」の新規追加
2014年10月24日 … 「モックテータ関数」の一部修正
2014年11月08日 … 「モックテータ関数」のグラフを変更（Ver.8 化）
2014年11月12日 … 「一般 Lamé 関数」の新規追加
2014年11月17日 … 「Lamé 固有値関数」のグラフを変更（Ver.8 化）
2015年01月06日 … 「Mathieu 関数」の全グラフを変更（Ver.8 化）
2015年01月13日 … 「ガンマ関数」の全グラフを変更（Ver.8 化）
2015年02月10日 … 「ゼータ関数」の全グラフを変更（Ver.8 化）
2015年03月12日 … 「ゼータ関数に関連する関数」の全グラフを変更（Ver.8 化）
2015年07月23日 … サイトのデザイン･レイアウト変更（マルチデバイス対応 他）
2015年07月23日 … 「Debye 関数」の新規追加
2015年07月23日 … 「ポリ対数関数」の全グラフを変更（Ver.8 化）
2015年08月17日 … 「回転楕円体波動関数」の全グラフを変更（Ver.8 化）
2015年10月09日 … 「多重ガンマ関数, 多重三角関数」の新規追加
2015年11月19日 … 「Lane - Emden 関数」の新規追加
2015年11月25日 … アニメーションの掲載を開始
2016年01月20日 … 「第2種 Painlevé 方程式の古典関数解」の修正
2016年01月20日 … 「高階 Painlevé 方程式の古典関数解」の新規追加
2016年02月24日 … 「Dedekind のゼータ関数」の新規追加
2016年02月29日 … 「Eichler のＬ関数」の新規追加
2016年03月23日 … 「第4種 Painlevé 方程式の古典関数解」の新規追加
2016年05月07日 … 「Coulomb 波動関数」の全グラフを変更（Ver.8 化）
2016年05月07日 … 「Hankel-Coulomb 波動関数」の新規追加
2016年05月11日 … 「Euler 和」の新規追加
2016年06月02日 … 「鎌倉・横浜の風景」の新規追加
2016年06月07日 … 「実解析的 Eisenstein 級数」の新規追加
2016年06月14日 … 「Riesz 関数」の新規追加
2016年08月03日 … 独自研究「素数正弦関数・素数ガンマ関数」の新規追加
2016年08月24日 … 「保型関数」の一部追加＆全グラフ変更（Ver.8 化）
2016年11月01日 … 「Heun 関数・合流型 Heun 関数」の新規追加
2016年11月24日 … 「Bessel 関数関連」の全グラフを変更（Ver.8 化）
2016年11月24日 … 「Lommel 関数」の新規追加
2017年02月10日 … 「Lorenz 関数」の新規追加
2017年04月12日 … 「Dedekind のゼータ関数」の一部追加
2017年06月01日 … 独自研究「非 Bohr-Mollerup 型ガンマ関数」の新規追加
2017年06月04日 … 「一般の保型関数」の新規追加
2017年07月30日 … 「Ｋ関数」の新規追加
2017年08月16日 … 「不完全ガンマ関数」の全グラフを変更（Ver.8 化）
2017年09月11日 … 「積分指数関数」の全グラフを変更（Ver.8 化）
2017年11月11日 … 独自研究「真性特異点を持つ二重周期関数」の新規追加
2018年01月04日 … 「素数ゼータ関数」の一部追加
2018年02月13日 … 「Clausen 関数・積分逆正接関数」の一部追加
2018年04月07日 … FunctionPlot.m の Mathematica Ver.6 以降での使用が可能に
2018年04月08日 … 「Debye 関数」の全グラフを変更
2018年06月20日 … 「誤差関数」の全グラフを変更（Ver.8 化）
2018年06月23日 … 独自研究「von Mangoldt 指数級数の漸近公式」の新規追加
2018年09月21日 … 「楕円積分」の全グラフを変更（Ver.8 化）
2018年09月28日 … グラフの凡例「等角写像図と多価関数の描画法」の新規追加
2018年12月22日 … 「楕円関数」の全グラフを変更（Ver.8 化）
2019年03月06日 … 独自研究「Kronecker 極限公式の導出方法」の新規追加
2019年04月10日 … 「楕円テータ関数」の全グラフを変更（Ver.8 化）
2019年08月14日 … 「楕円モジュラー関数」の全グラフを変更（Ver.8 化）
2019年08月25日 … 「ガンマ関数」の一部追加（Hadamard, 交互階乗）
2019年08月29日 … Questions「連分数＋級数型の表示式」の追加
2019年12月04日 … 「Riemann 素数計数関数」の一部変更
2019年12月13日 … 「保型関数」の一部変更
2019年12月19日 … アニメーションのコードを掲載
2020年04月30日 … 「Bessel 関数」の全グラフを変更（Ver.8 化）
2020年08月02日 … 「積分 Bessel 関数」の全グラフを変更（Ver.8 化）
2020年11月04日 … 「Legendre 関数」の全グラフを変更（Ver.8 化）
2020年12月10日 … 「三次元座標系一覧」の内容を拡充
2020年12月22日 … 「Legendre 関数に関連する関数」の全グラフを変更（Ver.8 化）
2021年03月24日 … 「Hermite 関数」の全グラフを変更（Ver.8 化）
2021年03月24日 … 応用編「調和振動子の存在確率」の全グラフを変更（Ver.8 化）
2021年05月16日 … Mathematica の落とし穴「等高線は悩ましい」を新規追加
2021年06月27日 … 「Laguerre 関数」の全グラフを変更（Ver.8 化）
2021年06月27日 … 応用編「水素原子における電子の存在確率」の全グラフを変更（Ver.8 化）
2021年07月21日 … 「三次元グラフを立体視の画像にする」の新規追加
2021年11月20日 … 「Bessel 関数関連」Airy-Hardy積分関数とグラフの追加
2022年01月28日 … 「Chebyshev 関数」の全グラフを変更（Ver.8 化）
2022年01月28日 … 「楕円有理関数・楕円 Chebyshev 関数」の新規追加
2022年06月12日 … 「Gegenbauer 関数」の全グラフを変更（Ver.8 化）
2022年11月30日 … 「超レムニスケート関数」の内容を拡充
2022年12月15日 … 「Squigonometric 関数」の新規追加
2023年03月14日 … 「Jacobi 関数」の全グラフを変更（Ver.8 化）
2023年03月14日 … 「Zernike 関数」の新規追加
2023年09月07日 … 「Wigner のD関数」の新規追加
2024年03月07日 … 「Coulomb 波動関数」の全グラフを変更（2回目）
2024年06月22日 … 独自研究「s＝4 および 3 における Fibonacci ゼータ関数の特殊値」の新規追加
【 Petite Galerie 】
前身および旧サイトのスクラップブック。